
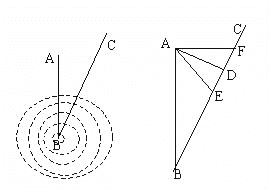
【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
【答案】(1)该城市会受到这次台风的影响;(2)这次台风影响该城市的持续时间为4![]() 小时;(3)当台风中心位于D处时,A城市所受这次台风的风力最大,其最大风力为6.5级.
小时;(3)当台风中心位于D处时,A城市所受这次台风的风力最大,其最大风力为6.5级.
【解析】
(1)过A作AD⊥BC于D,在Rt△ABD中,根据30°的锐角所对的直角边等于斜边的一半求得AD的长,再与受台风影响范围的半径比较即可求得结论;(2)受台风影响时,台风中心移动的距离,应该是A为圆心,台风影响范围的半径为半径,所得圆截得的BC上的线段的长即EF得长,根据勾股定理及等腰三角形的性质求得EF的长,再根据时间=路程÷速度即可求解;(3)因AD最短,所以风力最大时,台风中心应该位于D点,然后根据题目给出的条件求解即可.
(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.
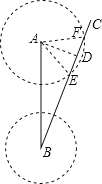
在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴AD=![]() AB=110,
AB=110,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12-4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2![]() =
=![]() .
.
∴台风影响该市的持续时间t=![]() ÷15=4
÷15=4![]() (小时).
(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12-(110÷20)=6.5(级).


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G. 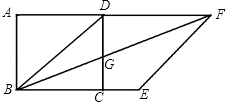
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所示是二次函数y=ax2+bx+c图像的一部分,图像过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )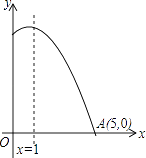
A.abc>0
B.当x<1时,y随x的增大而增大
C.a+b+c>0
D.方程ax2+bx+c=0的根为x1=﹣3,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() 与双曲线y=
与双曲线y= ![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= ![]() 向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y= ![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )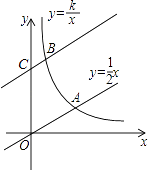
A.3
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P. 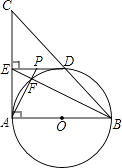
(1)求证:DE是⊙O的切线;
(2)求tan∠ABE的值;
(3)若OA=2,求线段AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D是⊙O上的四点,∠BAC=∠CAD,P是线段CD延长线上一点,且∠PAD=∠ABD.
(1)请判断△BCD的形状(不要求证明);
(2)求证:PA是⊙O的切线;
(3)求证:AP2﹣DP2=DPBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.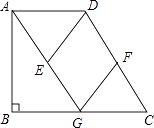
(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com