
【题目】如图,A,B,C,D是⊙O上的四点,∠BAC=∠CAD,P是线段CD延长线上一点,且∠PAD=∠ABD.
(1)请判断△BCD的形状(不要求证明);
(2)求证:PA是⊙O的切线;
(3)求证:AP2﹣DP2=DPBC.
【答案】
(1)
解:∵∠BAC=∠CAD,
∴ ![]() ,
,
∴∠BDC=∠CBD,
∴△BCD是等腰三角形
(2)
证明:连接OA、OD,
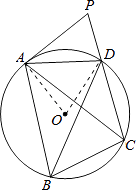
则∠AOD=180°﹣2∠OAD,
∵∠AOD=2∠ABD=2∠PAD,
∴∠PAD=90°﹣∠OAD,
∴∠PAD+∠OAD=90°,
∴OA⊥AP,
∴PA是⊙O的切线.
(3)
证明:∵PA是⊙O的切线,
∴AP2=PD×PC,
∴AP2﹣DP2=PD×PC﹣DP2=DP(PC﹣DP)=DP×CD,
又∵BC=CD,
∴AP2﹣DP2=DPBC.
【解析】(1)由圆周角定理可得∠BDC=∠BAC,再由∠BAC=∠CAD,可判断△BCD的形状;(2)连接OA、OD,则可得∠AOD=180°﹣2∠OAD,再由∠AOD=2∠ABD=2∠PAD,可得∠PAD=90°﹣∠OAD,从而可得OA⊥AP,判断出结论.(3)应用切割线定理可得AP2=PD×PC,然后提取公因式DP后,可得出等式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | |
销售玩具获得利润w(元) |
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
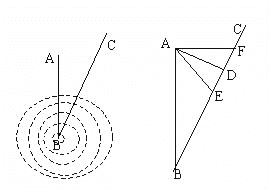
【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】韦玲和覃静两人玩“剪刀、石头、布”的游戏,游戏规则为:剪刀胜布,布胜石头,石头胜剪刀. 
(1)请用列表法或树状图表示出所有可能出现的游戏结果;
(2)求韦玲胜出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.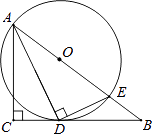
(1)求证:点D在⊙O上;
(2)求证:BC是⊙O的切线;
(3)若AC=6,BC=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
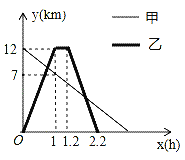
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com