
����Ŀ��ij�̳���Ӫij��Ʒ�Ƶ���ߣ�����ʱ�ĵ�����30Ԫ�������г����飺��һ��ʱ���ڣ����۵�����40Ԫʱ����������600���������۵���ÿ��1Ԫ���ͻ����۳�10����ߣ�
��1�����������Ʒ����ߵ����۵���ΪxԪ��x��40��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ����������wԪ�����ѽ����д�ڱ����У�
���۵��ۣ�Ԫ�� | x |
������y������ | |
������������w��Ԫ�� |
��2���ڣ�1���������£����̳������10000Ԫ�����������������۵���xӦ��Ϊ����Ԫ��
��3���ڣ�1���������£�����߳��涨��Ʒ��������۵��۲�����44Ԫ�����̳�Ҫ��ɲ�����540���������������̳����۸�Ʒ�����õ���������Ƕ��٣�
���𰸡�
��1���⣺
���۵��ۣ�Ԫ�� | x |
������y������ | 1000��10x |
������������w��Ԫ�� | ��10x2+1300x��30000 |
��2���⣺��10x2+1300x��30000=10000
��֮�ã�x1=50��x2=80
��������۵���Ϊ50Ԫ��80Ԫʱ���ɻ��10000Ԫ��������
��3���⣺��������� ![]()
��֮�ã�44��x��46��
w=��10x2+1300x��30000=��10��x��65��2+12250��
��a=��10��0���Գ�����ֱ��x=65��
�൱44��x��46ʱ��w��x���������
�൱x=46ʱ��W���ֵ=8640��Ԫ����
���̳����۸�Ʒ�����õ��������Ϊ8640Ԫ
����������1�������۵���ÿ��1Ԫ���ͻ����۳�10����ߵ�y=600����x��40����10=1000��10x������=��1000��10x����x��30��=��10x2+1300x��30000����2���10x2+1300x��30000=10000�����x��ֵ���ɣ���3���������x��ȡֵ��Χ��Ȼ���w=��10x2+1300x��30000ת����y=��10��x��65��2+12250�����x��ȡֵ��Χ������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��ԶԽ���BDΪ��������BDFE��ʹB��C��E������ͬһֱ���ϣ�����BF����CD���G�� 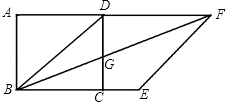
��1����֤��CG=CE��
��2���������α߳�Ϊ4��������BDFE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������������Ϣ�� ��ab��0����a+b+c��0����b+2c��0����a��2b+4c��0���� ![]() ��
��
����Ϊ������ȷ��Ϣ�ĸ����У� ��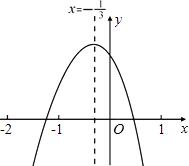
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Կ�չ��ѧ��ÿ�����1Сʱ���������ij��ѧ����ѧУʵ���������������A����ӣ�B������C���ܲ���D�����������˶���Ŀ��Ϊ���˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼͳ��ͼ������ͼ����Ϣ����������⣺
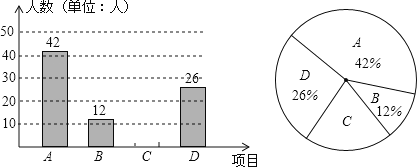
��1����У���ε����У��������˶�����ѧ����
��2���뽫����ͳ��ͼ����������
��3���ڱ��ε����ѧ���������ȡ1�ˣ���ϲ�����ܲ����ĸ����ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾���ԭ��o��x����һ��A��4��0���������߶���ΪE�����ĶԳ�����x�ύ�ڵ�D��ֱ��y=��2x��1������������һ��B����2��m������y�ύ�ڵ�C���������ߵĶԳ��ύ�ڵ�F��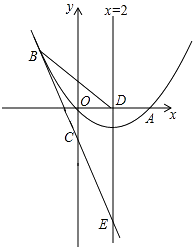
��1����m��ֵ���������߶�Ӧ�Ľ���ʽ��
��2��P��x��y�����������ϵ�һ�㣬��S��ADP=S��ADC �� ������з��������ĵ�P�����ꣻ
��3����Q��ƽ��������һ�㣬��M�ӵ�F�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������M���˶�ʱ��Ϊt�룬�Ƿ���ʹ��Q��A��E��M�ĵ�Ϊ������ı��������Σ����ܣ���ֱ��д����M���˶�ʱ��t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A��5��0�����Գ���Ϊֱ��x=1�����н����д�����ǣ� ��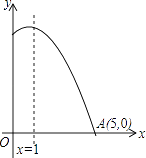
A.abc��0
B.��x��1ʱ��y��x�����������
C.a+b+c��0
D.����ax2+bx+c=0�ĸ�Ϊx1=��3��x2=5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y= ![]() ��˫����y=
��˫����y= ![]() ��k��0��x��0�����ڵ�A����ֱ��y=
��k��0��x��0�����ڵ�A����ֱ��y= ![]() ����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y=
����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y= ![]() ��k��0��x��0�����ڵ�B����OA=3BC����k��ֵΪ��������
��k��0��x��0�����ڵ�B����OA=3BC����k��ֵΪ��������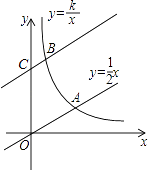
A.3
B.6
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��D�ǡ�O�ϵ��ĵ㣬��BAC=��CAD��P���߶�CD�ӳ�����һ�㣬�ҡ�PAD=��ABD��
��1�����жϡ�BCD����״����Ҫ��֤������
��2����֤��PA�ǡ�O�����ߣ�
��3����֤��AP2��DP2=DPBC��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com