
【题目】如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
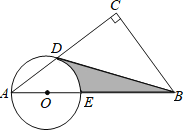
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,DE,求出∠ADE=90°=∠C,推出DE∥BC,求出∠EDB=∠CBD=∠A,根据∠A+∠OED=90°,求出∠EDB+∠ODE=90°,根据切线的判定推出即可;
(2)分别求出扇形DOE和△ODB的面积,即可求出答案.
解:(1)直线BD与⊙O的位置关系是相切
证明:连接OD、DE

∵∠C=90°
∴∠CBD+∠CDB=90°
∵∠A=∠CBD
∴∠A+∠CDB=90°
∵OD=OA
∴∠A=∠ADO
∴∠ADO+∠CDB=90°
∴∠ODB=180°﹣90°=90°
∴OD⊥BD
∵OD为半径
∴BD是⊙O切线
(2)解:∵AE是⊙O直径
∴∠ADE=90°
∵AE=4,∠A=30°
∴DE=![]() AE=2,∠AED=60°
AE=2,∠AED=60°
∵OD=OE
∴△DOE是等边三角形
∴∠ODE=60°,OD=OE=DE=2
∵∠ODB=90°
∴∠EDB=30°
∴∠B=∠DEO﹣∠EDB=60°﹣30°=30°
∴OB=2OD=4
由勾股定理得:DB=![]() ,
,
∴阴影部分的面积S=S△ODB﹣S扇形DOE
=![]()
=![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
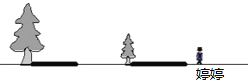
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
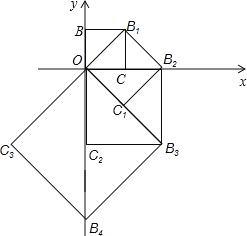
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,再以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2,依次下去,则点B7的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=![]() x与抛物线交于A、B两点,直线l为y=﹣1.
x与抛物线交于A、B两点,直线l为y=﹣1.
(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
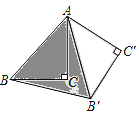
【题目】如图,在△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A逆时针方向旋转60°到△AB'C'的位置,则图中阴影部分的面积是( )
,将△ABC绕点A逆时针方向旋转60°到△AB'C'的位置,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
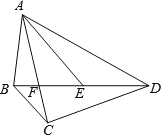
【题目】如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.
(1)求证:△ABE∽△ACD;
(2)若BC=2,AD=6,DE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
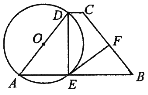
【题目】梯形ABCD中,AB∥DC,AD=BC,以AD为直径的⊙O交AB于E,⊙O的切线EF交BC于F,求证:
(1)EF⊥BC; (2)BF·BC=BE·AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com