
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.

【答案】(1)可分割成8个小正方形;(2)n所有可能的值为60或52或53;(3)当n>3时,此长方形可分割成小正方形为:当n=3k时,有k个小正方形;当n═3k+1时,有(k+3)个小正方形;当n=3k+2时,有(k+3)个小正方形.
【解析】
根据题意,继续画图分析并总结规律,然后再解决下列问题即可.
(1)根据以上结论即可求解;
(2)根据以上结论即可求解;
(3)根据总结规律整理到一起即可.
解:若n=4=3×1+1时,如下图所示,此时共有4=(1+3)个小正方形

若n=7=3×2+1时,如下图所示,此时共有5=(2+3)个小正方形

由上可知:当n等于3的k倍加1时,小正方形的个数为(k+3)个,即当n═3k+1时,有(k+3)个小正方形;
若n=5=3×1+2时,如下图所示,此时共有4=(1+3)个小正方形

若n=8=3×2+2时,如下图所示,此时共有5=(2+3)个小正方形

由上可知: 当n等于3的k倍加2时,小正方形的个数为(k+3)个,即当 n=3k+2时,有(k+3)个小正方形;
若n=6=3×2时,如下图所示,此时共有2个小正方形

若n=9=3×3时,如下图所示,此时共有3个小正方形

由上可知: 当n等于3的k倍时,小正方形的个数为k个,即 n=3k时,有k个小正方形;
(1)n=16=3×5+1时,可分割成5+3=8个小正方形;
(2)当长方形被分割成20个小正方形时,
若n=3k时,此时k=20,代入解得:n=60;
若n═3k+1时,此时k+3=20,解得k=17,代入解得:n═52;
若n=3k+2时,此时k+3=20,解得k=17,代入解得:n═53.
综上所述:n所有可能的值为60或52或53;
(3)由上可知:当n>3时,此长方形可分割成小正方形为:
当n=3k时,有k个小正方形;
当n═3k+1时,有(k+3)个小正方形;
当n=3k+2时,有(k+3)个小正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
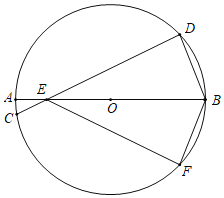
【题目】如图所示,⊙O的直径AB和弦CD相交于点E,且点B是劣弧DF的中点.
(1)求证:△EBD≌△EBF;
(2)已知AE=1,EB=5,∠DEB=30°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
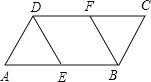
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
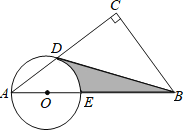
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C.
轴交于点C.
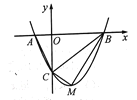
(1)请求出抛物线顶点M的坐标(用含k的代数式表示)以及A,B两点的坐标.
(2)试探究△BCM与△ABC的面积比值是否不变,若不变,试求出这个比值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
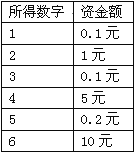
【题目】有时我们可以看到这样的转盘游戏:如图所示,你只要出1元钱就可以随意地转动转盘,转盘停止时指针落在哪个区域,你就按照这个区域所示的数字相应地顺时针跳过几格,然后按照下图所示的说明确定你的资金是多少.例如,当指针指向 “2”区域时候,你就向前跳过两个格到“5”,按奖金说明,“5”所示的资金为0.2元,你就可以得0.2元.请问这个游戏公平吗?能否用你所学的知识揭示其中的秘密?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com