
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的性质证明△ABE≌△BCF,可证得①AE⊥BF;②AE=BF正确;证明△BGE∽△ABE,可得![]() =
=![]() =
=![]() ,故③不正确;由S△ABE=S△BFC可得S四边形CEGF=S△ABG,故④正确.
,故③不正确;由S△ABE=S△BFC可得S四边形CEGF=S△ABG,故④正确.
解:在正方形ABCD中,AB=BC,∠ABE=∠C=90,
又∵BE=CF,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∴∠FBC+∠BEG=∠BAE+∠BEG=90°,
∴∠BGE=90°,
∴AE⊥BF,故①,②正确;
∵CF=2FD,BE=CF,AB=CD,
∴![]() =
=![]() ,
,
∵∠EBG+∠ABG=∠ABG+∠BAG=90°,
∴∠EBG=∠BAE,
∵∠EGB=∠ABE=90°,
∴△BGE∽△ABE,
∴![]() =
=![]() =
=![]() ,即BG=
,即BG=![]() GE,故③不正确,
GE,故③不正确,
∵△ABE≌△BCF,
∴S△ABE=S△BFC,
∴S△ABES△BEG=S△BFCS△BEG,
∴S四边形CEGF=S△ABG,故④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k+1)x+k2﹣2=0
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两个实数根为x1、x2,且满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=6,BC=8,D边BC上的任意一点,将∠C沿过点D的直线折叠,使点C落在斜边AB上的点E处,当△BDE是直角三角形时,CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D为等腰Rt△ABC斜边AB的中点,DM⊥DN,DM,DN分别交BC,CA于点E,F.
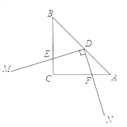
(1)当∠MDN绕点D转动时,求证:DE=DF.
(2)若AB=2,求四边形DECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
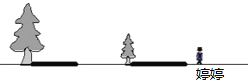
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
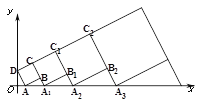
【题目】在平面直角坐标系![]() 中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com