
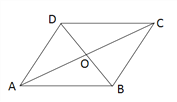
【题目】如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.求BC的长和四边形ABCD的面积.
【答案】BC的长为12,四边形ABCD的面积为120
【解析】试题分析:根据勾股定理求得OA的长,再根据对角线互相平分的四边形是平行四边形证明四边形ABCD是平行四边形,从而根据平行四边形的对边相等就可求得BC的长;根据平行四边形的面积公式可以求得它的面积.
试题解析:在△AOD中,∠ADB=90°,AD=12,0D=5,
根据勾股定理,得
OA2=OD2+AD2=52+122=169,
∴OA=13.
∵AC=26,OA=13,
∴OA=OC,
又DO=OB,
∴四边形ABCD为平行四边形,
∴AD=BC=12;
∵∠ADB=90°,
∴AD⊥BD,
∴S四边形ABCD=ADBD=12×10=120,
答:BC的长为12,四边形ABCD的面积为120.


科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,
证明你的结论.
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形;
(3)当四边形ABCD的对角线满足_____条件时,四边形EFGH是菱形;
(4)你学过的哪种特殊四边形的中点四边形是矩形?_____;
(5)你学过的哪种特殊四边形的中点四边形是菱形?_____;
(6)你学过的哪种特殊四边形的中点四边形是正方形?_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
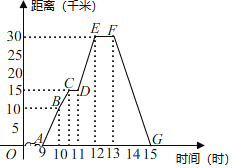
【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系,王勇9点离开家,15点回家,请结合图象,回答下列问题:
![]() 到达离家最远的地方是什么时间?离家多远?
到达离家最远的地方是什么时间?离家多远?
![]() 他一共休息了几次?休息时间最长的一次是多长时间?
他一共休息了几次?休息时间最长的一次是多长时间?
![]() 在哪些时间段内,他骑车的速度最快?最快速度是多少?
在哪些时间段内,他骑车的速度最快?最快速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是(填编号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一元二次方程x2﹣3x+m﹣1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程有两个相等的实数根,求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的表达式为
的表达式为![]() ,直线
,直线![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() :
:![]() 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求m的值;
(2)求直线![]() 的表达式;
的表达式;
(3)根据图象,直接写出![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
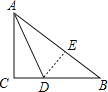
【题目】如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com