
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
【答案】
(1)100;108°
(2)解:如图所示: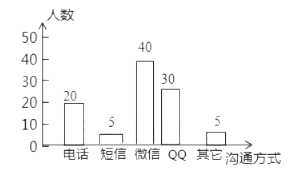
(3)解:喜欢用微信沟通所占百分比为: ![]() ×100%=40%,
×100%=40%,
∴该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有:1500×40%=600人;
(4)解:列出树状图,如图所示: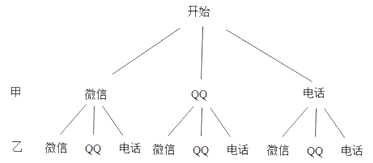
所有情况共有9种情况,其中两人恰好选中同一种沟通方式共有3种情况,甲、乙两名同学恰好选中同一种沟通方式的概率为: ![]() =
= ![]() .
.
【解析】(1)喜欢用电话沟通的人数为20,所占百分比为20%,∴此次共抽查了:20÷20%=100人,喜欢用QQ沟通所占比例为: ![]() =
= ![]() ,
,
∴QQ”的扇形圆心角的度数为:360°× ![]() =108°;
=108°;
(2)喜欢用短信的人数为:100×5%=5人,喜欢用微信的人数为:100﹣20﹣5﹣30﹣5=40.
补充图形,如图所示:
(1)共抽查的学生=电话的人数除以电话所占的百分比;表示“QQ”的扇形圆心角的度数=360°乘以“QQ”所占百分比,计算即可得出答案。
(2)分半求出喜欢用短信的人数和喜欢用微信的人数,再补全条形统计图即可。
(3)先求出用微信的学生所占百分比,再用该校的学生人数乘以微信的学生所占百分比,计算即可得出答案。
(4)根据题意列出树状图,求出所有可能的结果数,再求出甲、乙两名同学恰好选中同一种沟通方式的可能数,然后根据概率公式求解即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料I:
教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则:
的两根,则:![]() __ _,
__ _,![]() __ _,那么_
__ _,那么_![]() (请你完成以上的填空)
(请你完成以上的填空)
阅读材料:II
已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)若![]() 且
且![]() 则
则![]() ;
;
(3)已知![]() 且
且![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,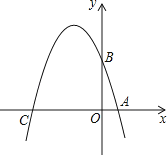
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
| 10 | 20 | 30 |
| 60 | 55 | 50 |
(1)求y与x之间的函数关系式;

(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明就市电视台的各节目所受欢迎的情况,对本班50名同学进行了一次调查,结果如下:
最受学生欢迎的电视节目
节目 | 人数 |
体育 | 18 |
新闻 | 16 |
综艺 | 8 |
动画 | 5 |
其他 | 3 |
(1)选用适当的统计图描述上表数据;
(2)还能用其他统计图描述吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6).
(1)求二次函数的解析式;
(2)画出它的图象;
(3)写出它的对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)11![]() -1
-1![]() -1
-1![]() +4
+4![]() ;
;
(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1![]() -
-![]() +2
+2![]() +
+![]() -4
-4![]() ;
;
(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在⊙O中. AE直径,AD是弦,B为AE延长线上--点,作BC⊥AD,与AD延长线交于点C.且∠CBD=∠A.
(1)判断直线BD与⊙0的位置关系,并证明你的结论;
(2)若∠A=30 ![]() ,OA=6,求图中阴影部分的面积.
,OA=6,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com