
| 2 |

| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
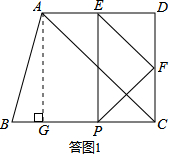
| AG |
| tanB |
| 8 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 10 |
| 7 |
| 10 |
| 3 |
| 10 |
| 7 |
| 10 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 12 |
| 1 |
| 22 |
| 3 |
| 1×2 |
| 1 |
| 1×2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 7 |
| 2×3 |
| 1 |
| 2×3 |
| 1 |
| 32 |
| 1 |
| 42 |
| 13 |
| 3×4 |
| 1 |
| 3×4 |
| a1 |
| a2 |
| a3 |
| a100 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
. |
| X |
. |
| X |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、抛掷一枚质地均匀的硬币,落地后正面朝上 |
| B、海安县7月份某一天的最低气温是-3℃ |
| C、通常加热到100℃时,水沸腾 |
| D、打开电视,正在播放综艺节目《一站到底》 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com