
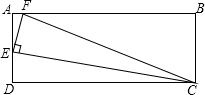
 矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.| EF |
| CE |
| AE |
| DC |
| 1 |
| 6 |
| EF |
| CE |
| 1 |
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 2 |
| 1 | ||
1-
|
| m-3 |
| 2m-4 |
| 5 |
| m-2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
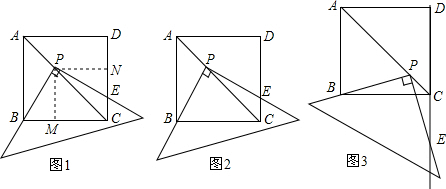
查看答案和解析>>
科目:初中数学 来源: 题型:
 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| p(p-a)(p-b)(p-c) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com