
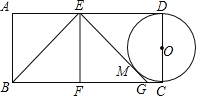
【题目】如图,在矩形ABCD中,AB=4,AD=8,点E、点F分别在边AD,BC上,且EF⊥AD,点B关于EF的对称点为G点,连接EG,若EG与以CD为直径的⊙O恰好相切于点M,则AE的长度为( )
A.3B.![]() C.6+
C.6+![]() D.6﹣
D.6﹣![]()
【答案】D
【解析】
设AE=x,则ED=8﹣x,易得四边形ABFE为矩形,则BF=x,利用对称性质得FG=BF=x,则CG=8﹣2x,再根据切线长定理得到EM=ED=8﹣x,GM=GC=8﹣2x,所以EG=16﹣3x,在Rt△EFG中利用勾股定理得到42+x2=(16﹣3x)2,然后解方程可得到AE的长.
解:设AE=x,则ED=8﹣x,
∵EF⊥AD,
∴四边形ABFE为矩形,
∴BF=x,
∵点B关于EF的对称点为G点,
∴FG=BF=x,
∴CG=8﹣2x,
∵∠ADC=∠BCD=90°,
∴AD和BC为⊙O的切线,
∵EG与以CD为直径的⊙O恰好相切于点M,
∴EM=ED=8﹣x,GM=GC=8﹣2x,
∴EG=8﹣x+8﹣2x=16﹣3x,
在Rt△EFG中,42+x2=(16﹣3x)2,
整理得x2﹣12x+30=0,
解得x1=6﹣![]() ,x2=6+
,x2=6+![]() (舍去),
(舍去),
即AE的长为6﹣![]() .
.
故选:D.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,点P在AB的延长线上,PC与⊙O相切于点C,点D为弧AC上的点,且2∠DAB﹣∠P=90°,连接AD.
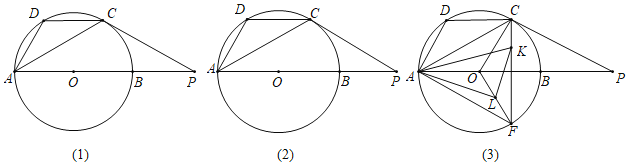
(1)如图1,求证:弧AD=弧BC;
(2)如图2,PC=6,PB=![]() ,求∠ADC度数;
,求∠ADC度数;
(3)如图3,在(2)的条件下,F为AB下方⊙O上一点.∠ACF=60°,L为OF中点,LK⊥AL于L,交CF于点K.连接AK,求AK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
(1)观察猜想
如图1,![]() 分别交
分别交![]() 于点
于点![]()
![]() 的值是 ,直线
的值是 ,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是 .
相交所成的较小角的度数是 .

(2)类比探究
如图2,将![]() 绕点
绕点![]() 逆时针旋转,请写出
逆时针旋转,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的小角的度数,并就图2的情形说明理由,
相交所成的小角的度数,并就图2的情形说明理由,
(3)解决问题
若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
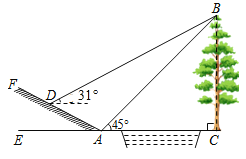
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
(1)求小明从点A走到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式为![]() (
(![]() 、
、![]() 、
、![]() 为常数,
为常数,![]() ),且
),且![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不同根
有两个不同根![]() 、
、![]() ,且
,且![]() ;④二次函数的图象与坐标轴有三个不同交点,其中正确的个数是( ).
;④二次函数的图象与坐标轴有三个不同交点,其中正确的个数是( ).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
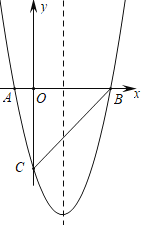
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0).B(5,0)两点,与y轴交于点C.
(1)求此物线的解析式;
(2)在此物线的对称轴上找一点M.使得MA+MC最小,请求出点M的坐标;
(3)在直线BC下方抛物线上是否存在点P,使得△PBC的面积最大?若存在.请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
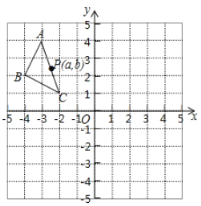
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标为
的三个顶点坐标为![]() ,
,![]() ,
,![]() ,
,![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() ,得到
,得到![]() ,
,![]() 向右平移6个单位,再向上平移2个单位得到
向右平移6个单位,再向上平移2个单位得到![]() .
.
(1)画出![]() 和
和![]() ;
;
(2)![]() 是
是![]() 的
的![]() 边上一点,
边上一点,![]() 经旋转、平移后点
经旋转、平移后点![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,请写出点
,请写出点![]() 、
、![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com