
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ�������ɽ��ʡ�����ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣�ij�̳��ƻ������ף������ֽ��ܵƹ�1200ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
(1)��ν�����������ǡ��Ϊ46000Ԫ?
(2)���̳��������ֽ��ܵ�xֻ������̳���������ܵ�ʱ������w�빺�����ֽ��ܵ�x֮��ĺ�����ϵʽ��
(3)��ν������̳���������ܵ�ʱ��������Ҳ����������۵�30%����ʱ����Ϊ����Ԫ?
���𰸡���1���������ͽ��ܵ�400ֻ�����ͽ��ܵ�800ֻ����2��w=��10x+18000����3���̳��������ͽ��ܵ�450ֻ�����ͽ��ܵ�750ֻ����������ܵ�ʱ����Ϊ13500Ԫ��
��������
��1�����̳�Ӧ�������ͽ��ܵ�xֻ�����������г����̽�ɣ�
��2�����̳�Ӧ�������ͽ��ܵ�xֻ�����������г���������ʽ���ɣ�
��3�����̳��������ͽ��ܵ�xֻ�������ͽ��ܵƣ�1200��x��ֻ�����ݡ��̳���������ܵ�ʱ��������Ҳ����������۵�30%���в���ʽ�����һ�κ��������ʽ�ɣ�
��1�����̳�Ӧ�������ͽ��ܵ�xֻ�������ͽ��ܵ�Ϊ��1200��x��ֻ����������ã�
25x+45��1200��x��=46000
��ã�x=400��
��x=400ʱ��1200��x=800��
�𣺹������ͽ��ܵ�400ֻ�����ͽ��ܵ�800ֻʱ��������ǡ��Ϊ46000Ԫ��
��2�����̳�Ӧ�������ͽ��ܵ�xֻ���̳��������������ܵƿɻ���wԪ��
��������ã�w=��30��25��x+��60��45����1200��x��=5x+18000��15x=��10x+18000
����w=��10x+18000��
��3�����̳��������ͽ��ܵ�xֻ�������ͽ��ܵƣ�1200��x��ֻ������ΪwԪ����������ã�
��10x+18000��[25x+45��1200��x��]��30%
��ã�x��450��
��w=��10x+18000����k=��10��0����w��x���������С����x=450ʱ��w���=13500Ԫ��
���̳��������ͽ��ܵ�450ֻ���������ͽ��ܵ�750ֻʱ���������Ϊ13500Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ�ABC�У���ACB=90�㣬��B=30�㣬AC=2 ![]() �����ǰ���ֱ�Ƕ���C��ʱ����ת������A�Ķ�Ӧ��A������AB�ߵ���ʼλ����ʱ��ֹͣת������B��ת����·����Ϊ�� ��
�����ǰ���ֱ�Ƕ���C��ʱ����ת������A�Ķ�Ӧ��A������AB�ߵ���ʼλ����ʱ��ֹͣת������B��ת����·����Ϊ�� �� 
A.![]() ��
��
B.![]() ��
��
C.2��
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ͬһ��·��˳������������A��B��C���ס��������οʹӾ���A�������ײ��е�����C���һ�20����ʱ���ŶӺ�˹۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ס��������뾰��A��·��s���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��
��1�����ٶ��� ��/���ӣ�
��2����20��t ��30ʱ�������뾰��A��·��s��t�ĺ�������ʽ��
��3���ҳ�����ʱ�������;��������
��4���������ᄚ��Cʱ�����뾰��C��·��Ϊ360�ף����ҴӾ���B���е�����C���ٶ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����AD�Ҳ���������ADEF������CF��
��1���۲����
��ͼ1������D���߶�BC��ʱ��
��BC��CF��λ�ù�ϵΪ�� ��
��BC��CD��CF֮���������ϵΪ������������ֱ��д�ں����ϣ�
��2����ѧ˼��
��ͼ2������D���߶�CB���ӳ�����ʱ�����ۢ٣����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����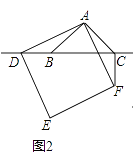
��3����չ����
��ͼ3������D���߶�BC���ӳ�����ʱ���ӳ�BA��CF�ڵ�G������GE������֪AB=2 ![]() ��CD=
��CD= ![]() BC�������GE�ij���
BC�������GE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC�У�FG��EB����2=��3����ô��EDB+��DBC���ڶ��ٶȣ�Ϊʲô��

�⣺��ΪFG��EB����֪����
����![]() ��__________����
��__________����
��Ϊ![]() ����֪����
����֪����
����![]() ��___________����
��___________����
����DE��BC ��__________����
����![]() ______��__________����
______��__________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ������������⣺
���·������:��ͼ��1������A��B�ֱ���ֱ��l���������㣬�����ֱ��l���ҵ�һ����C��ʹ�õ�C����A����B�ľ������̣�����ֻ������AB����ֱ��l�ཻ��һ�㣬��֪������㼴Ϊ����
��ͼ��2���������A��B�ֱ���ֱ��lͬ��������㣬�����l���ҵ�һ����C��ʹ������㵽��A����B�ľ������̣����ǿ���������ԳƵ����ʣ�������B���ڵĶԳƵ�B����ʱ����ֱ��l�ϵ���һ��C��������CB��CB���Ӷ������⣨2����Ϊ���⣨1������ˣ��߶�AB��ֱ��l�Ľ���C��λ�ü�Ϊ����
Ϊ��˵����C��λ�ü�Ϊ�������Dz�����ֱ����������ȡһ��C�䣬����AC�䣬BC�䣬B��C�䣮��ΪAB����AC��+C��B������AC+CB��AC'+C��B����AC+BC��С��
����
��ѧ˼��
��1�������л��߲��ֵ��������� ����
��2�������н��ͼ��2����ʾ�������ֵ���ѧ˼������ ����������ĸ���ż��ɣ�
A��ת��˼��
B����������˼��
C������˼��
Ǩ��Ӧ��
��3����ͼ����Rt��ABC�У���C��90�㣬��BAC��15�㣬��PΪC���ϵĶ��㣬��DΪAB���ϵĶ��㣬��AB��8cm����BP+DP����СֵΪ�� ��cm��
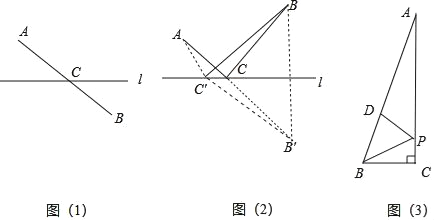
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ⱥ����ι���������![]() ������������Ϊ10Ԫ
������������Ϊ10Ԫ![]() ��8Ԫ
��8Ԫ![]() ���ҵڶ��αȵ�һ�ζึ��800Ԫ.
���ҵڶ��αȵ�һ�ζึ��800Ԫ.
��1���ó��������ι����İ����ֱ��Ƕ��ٶ֣�
��2�����ж���![]() ������14Ԫ
������14Ԫ![]() �ı��������
�ı��������![]() ��ʣ�µİ���ȫ�������۳����ϼƻ������4570Ԫ���ʳ��ж�ʣ�µİ����������ۣ�������=����������-�����ܳɱ���
��ʣ�µİ���ȫ�������۳����ϼƻ������4570Ԫ���ʳ��ж�ʣ�µİ����������ۣ�������=����������-�����ܳɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�ǵȱ�������ABC�ڵ�һ�㣬����PA��PB��PC����BPΪ������PBQ=60�㣬��BQ=BP������CQ.��PA��PB��PC=3��4��5������PQ�����жϡ�PQC����״�� ��

A. ֱ�������� B. ���������� C. ��������� D. �۽�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ת�̱����ֳ�4����ͬ��С���Σ����ֱ��������1��2��3��4���ֱ�ת������ת�̣�ת��ֹͣ��ָ����ָ���������Ϊֱ������ϵ��M������꣨��һ���������꣬�ڶ����������꣩��ָ�����ָ��ֽ����ϣ���Ϊָ��������ε����֣����M����ֱ��y=x���·��ĸ���Ϊ�� �� 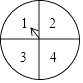
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com