
【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
【答案】(1)115°;(2)∠BOC=90°+![]() ∠A.
∠A.
【解析】试题分析:(1)根据三角形的内角和得到∠ABC+∠ACB=180°-∠A=130°,由于BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,根据三角形的内角和即可得到结论;
∠ACB,根据三角形的内角和即可得到结论;
(2)根据∠ABC与∠ACB的平分线相交于点O,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,于是得到∠OBC+∠OCB=
∠ACB,于是得到∠OBC+∠OCB=![]() (∠ABC+∠ACB),根据三角形内角和即可得到结论.
(∠ABC+∠ACB),根据三角形内角和即可得到结论.
试题解析:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△OBC中,
∠BOC=180°-(∠OBC+∠OCB)
=180°-![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°-![]() (180°-∠A)
(180°-∠A)
=90°+![]() ∠A,
∠A,
即∠BOC=90°+![]() ∠A.
∠A.
考点:三角形内角和定理.


科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
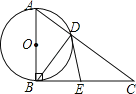
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明ED与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣1,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为m,四边形AOBC的周长为 (用含m的式子表示).
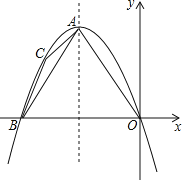
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
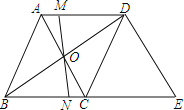
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某省遭遇历史罕见的夏秋东连旱,全省因灾造成直接经济损失68.77亿元,用科学计数法表示为( )
A、68.77×109 B、6.877×109 C、6.877×1010 D、6877×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,现用“☆”定义一种运算:a☆b=a2﹣b2,根据这个定义,代数式(x+y)☆y可以化简为( )
A. xy+y2 B. xy﹣y2 C. x2+2xy D. x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() =1﹣
=1﹣![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ﹣
﹣![]()
将以上三个等式两边分别相加得:![]() +
+![]() +
+![]() =1﹣
=1﹣![]() +
+![]() +
+![]() ﹣
﹣![]() =1﹣
=1﹣![]() =
=![]()
(1)按照一定规律排列式子:![]() +
+![]() +
+![]() +
+![]() +…,其中第n项(n为正整数)的形式为 ,按照材料中的写法,该项可表示为
+…,其中第n项(n为正整数)的形式为 ,按照材料中的写法,该项可表示为 ![]() ﹣
﹣![]() .
.
(2)直接写出下式:![]() +
+![]() +
+![]() +…+
+…+![]() 的计算结果为 .
的计算结果为 .
(3)探究并计算:![]() +
+![]() +…+
+…+![]() (其中n为正整数).
(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
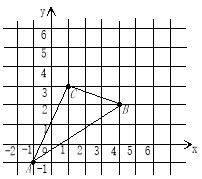
(1)请写出△ABC各点的坐标。(2)求出S△ABC(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com