
【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
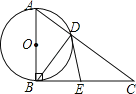
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明ED与⊙O相切.
【答案】(1)BC=![]() ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)根据勾股定理易求AB的长;根据△ABD∽△ACB得比例线段可求BC的长.
(2)连接OD,证明DE⊥OD.
(1)解:∵AB为直径,
∴∠ADB=90°,即BD⊥AC.
在Rt△ADB中,∵AD=3,BD=4,
∴由勾股定理得AB=5.
∵∠ABC=90°,BD⊥AC,
∴△ABD∽△ACB,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴BC=![]() ;
;
(2)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD;
又∵E是BC的中点,BD⊥AC,
∴DE=BE,
∴∠EDB=∠EBD.
∴∠ODB+∠EDB=∠OBD+∠EBD=90°,
即∠ODE=90°,
∴DE⊥OD.
∴ED与⊙O相切.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一种童装,平均每天可售出20件,每件盈利40元。经市场调查发现,若每件降价1元,则平均每天可多售2件。该商场要保证每天盈利1200元,同时又使顾客得到实惠,那么每件应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
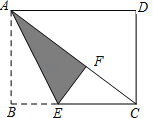
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏省占地面积约为107200平方公里.将107200用科学记数法表示应为( )
A.0.1072×106 B.1.072×105 C.1.072×106 D.10.72×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
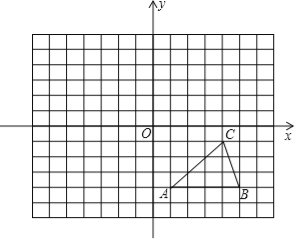
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
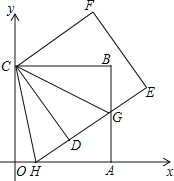
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸上,只用直尺画图.

(1)过点P作直线CD∥AB.
(2)作EB⊥AB,交直线CD于E点.
(3)过点P作出点P到直线AB的垂线段PQ,垂足为点Q,并量出点P到直线AB的距离(精确到0.1cm).
(4)比较线段BE与线段PQ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com