
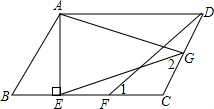
 已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知:在?ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.分析 (1)通过证△ECG≌△DCF得到CG=CF,结合已知条件知CG=$\frac{1}{2}$CD,即G为CD的中点.
(2)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可.
解答 (1)证明:如图,∵点F为CE的中点,
∴CF=$\frac{1}{2}$CE
在△ECG与△DCF中,
$\left\{\begin{array}{l}{∠2=∠1}\\{∠C=∠C}\\{CE=CD}\end{array}\right.$,
∴△ECG≌△DCF(AAS),
∴CG=CF=$\frac{1}{2}$CE.
又CE=CD,
∴CG=$\frac{1}{2}$CD,
即G为CD的中点;
(2)解:∵CE=CD,点F为CE的中点,CF=2.5,
∴DC=CE=2CF=5,
∵四边形ABCD是平行四边形,
∴AB=CD=5,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=$\sqrt{{5}^{2}-{4}^{2}}$=3.
点评 本题考查了平行四边形性质,勾股定理的运用,全等三角形的性质和判定等知识点的应用,主要考查学生综合运用定理进行推理的能力.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
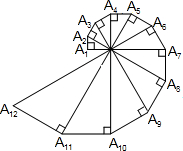 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
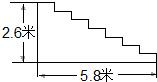 某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要多少元?
某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com