Question

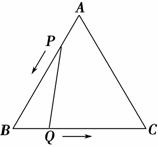
已知，如图，△ABC是边长为3 cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1 cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t(s)，解答下列问题：

(1)当t为何值时，△PBQ是直角三角形？

(2)设四边形APQC的面积为y(cm²)，求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的？如果存在，求出相应的t值；若不存在，说明理由．

Answer 1

解　(1)当∠BPQ＝90°时，

在Rt△BPQ中，∠B＝60°，BP＝3－t，BQ＝t.

∵cos B＝，∴BP＝BQ·cos B，

即3－t＝t·.解之，得t＝2.

当∠BQP＝90°时，

在Rt△BPQ中，∠B＝60°，BP＝3－t，BQ＝t，

∵cos B＝，∴BQ＝BP·cos B，即t＝(3－t)·.解之，得t＝1.

综上，t＝1或t＝2时，△PBQ是直角三角形．

(2)∵S_{四边形APQC}＝S_△ABC－S_△PBQ，

∴y＝×3×3·sin 60°－×(3－t)·t·sin 60°

＝t²－t＋.

又∵S_{四边形APQC}＝S_△ABC，

∴t²－＋＝×，

整理得，t²－3t＋3＝0，Δ＝(－3)²－4×1×3＜0，

∴方程无实根．∴无论t取何值时，四边形APQC的面积都不可能是△ABC面积的.