【题目】如图，是某广场台阶（结合轮椅专用坡道）景观设计的模型，以及该设计第一层的截面图，第一层有十级台阶，每级台阶的高为0.15米，宽为0.4米，轮椅专用坡道AB的顶端有一个宽2米的水平面BC；《城市道路与建筑物无障碍设计规范》第17条，新建轮椅专用坡道在不同坡度的情况下，坡道高度应符合以下表中的规定：

坡度

1：20

1：16

1：12

最大高度（米）

1.50

1.00

0.75

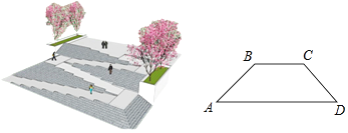
（1）选择哪个坡度建设轮椅专用坡道AB是符合要求的？说明理由；

（2）求斜坡底部点A与台阶底部点D的水平距离AD．

参考答案：

【答案】斜坡底部点A与台阶底部点D的水平距离AD为62米

【解析】试题分析：（1）计算最大高度为：0.15×10=1.5（米），由表格查对应的坡度即可做出判断；

（2）作梯形的高BE、CF，由坡度计算出AE、DF的长，相加即可得AD的长.

试题解析：（1）∵第一层有十级台阶，每级台阶的高为0.15米，

∴最大高度为0.15×10=1.5（米），

由表知建设轮椅专用坡道AB选择符合要求的坡度是1：20；

（2）如图，过B作BE⊥AD于E，过C作CF⊥AD于F，

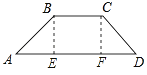
∴BE=CF=1.5，EF=BC=2，

∵，

∴，

∴AE=DF=30，

∴AD=AE+EF+DF=60+2=62，

答：斜坡底部点A与台阶底部点D的水平距离AD为62米.

关闭