
分析 先把2+$\sqrt{3}$化成$\frac{4+2\sqrt{3}}{2}$,其中4+2$\sqrt{3}$=3+2$\sqrt{3}$+1=($\sqrt{3}$+1)2,代入计算,进行分母有理化,得出结果.
解答 解:$\frac{1}{2(\sqrt{3}+\sqrt{2})}$+$\sqrt{2+\sqrt{3}}$,
=$\frac{\sqrt{3}-\sqrt{2}}{2(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\sqrt{\frac{4+2\sqrt{3}}{2}}$,
=$\frac{\sqrt{3}-\sqrt{2}}{2}$+$\frac{\sqrt{3}+1}{\sqrt{2}}$,
=$\frac{\sqrt{3}-\sqrt{2}+\sqrt{6}+\sqrt{2}}{2}$,
=$\frac{\sqrt{3}+\sqrt{6}}{2}$.
点评 本题考查了二次根式的加减法和分母有理化,同时还考查子完全平方公式在二次根式的运用,熟练掌握分母有理化,知道$\sqrt{3}$+$\sqrt{2}$的有理化因式为$\sqrt{3}$-$\sqrt{2}$;此题有难度,要注意$\sqrt{2+\sqrt{3}}$的变形.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
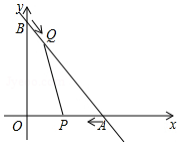 如图,直线y=-$\frac{4}{3}$x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
如图,直线y=-$\frac{4}{3}$x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
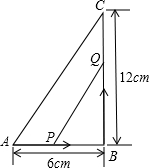 如图,在△ABC中,∠B=90°,点P从点B开始沿BA边向点A以1cm/s的速度移动,Q从点C开始沿CB边向B点以2cm/s的速度移动.如果点P、Q分别从B、C同时出发.
如图,在△ABC中,∠B=90°,点P从点B开始沿BA边向点A以1cm/s的速度移动,Q从点C开始沿CB边向B点以2cm/s的速度移动.如果点P、Q分别从B、C同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
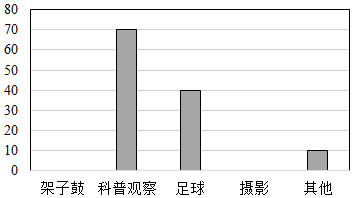 为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):
为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):| 选择 意向 | 架子鼓 | 科普观察 | 足球 | 摄影 | 其他 |
| 所占 百分比 | 30% | a | b | 10% | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
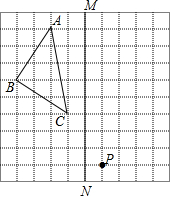 如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com