
【题目】如图,⊙O是以Rt△ABC的直角边AC 为直径的圆,与斜边AB相交于点D,过D作DH⊥AC,垂足为H,又过D点作直线交BC于E,使∠HDE = 2∠A.求证:
(1) DE是⊙O的切线;(2) OE是Rt△ABC的中位线.

【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)连接OD,通过三角形的外角证出∠HDE =∠HOD,再根据垂直定义利用等量代换证出∠HDE +∠ODH = 90,即可通过垂直证明结论.
(2)通过全等证出OE∥AB,再根据O是AC中点,即可得到结论.
证明:(1) 连结OD,则OD是⊙O的半径.
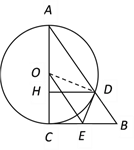
∵ ∠HDE = 2∠A,∠DOH = 2∠A,∴ ∠HDE =∠HOD.
∵ DH⊥AC,∴ ∠DOH +∠ODH = 90,
∴ ∠HDE +∠ODH = 90, 即OD⊥DE. ∴DE是⊙O的切线.
(2) ∵ DE是⊙O的切线,
∴ ∠ODE = 90,又OC = OD,OE = OE,
∴ △ODE≌△OCE, ∴ ∠COE =∠DOE.
又 ∵ ∠COD = 2∠A, ∴ ∠COE =∠A,
∴ OE∥AB,又AO = OC,
∴ OE是Rt△ABC的中位线.


科目:初中数学 来源: 题型:
【题目】将函数y=x2-2x-3的图象沿y轴翻折后与原图像合起来,构成一个新的函数的图象,若y=m与新图象有四个公共点,则m的取值范围为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( ) 
A.∠BAC=70°
B.∠DOC=90°
C.∠BDC=35°
D.∠DAC=55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com