
分析 (1)甲中x表示每天批发x吨;
(2)乙中$\frac{500}{x}$×(1+25%)”表示的意义是每天零售加批发的销量;
解决问题:设每天批发x吨,由题意得等量关系:全部批发所用时间-批发价零售所用时间=5,根据等量关系列出方程,再解即可;
拓展反思,根据题意可得批发所赚总利润,批发加零售所赚总利润:再计算增加百分比即可.
解答 解:(1)在甲所列的方程中,未知数“x”表示的意义是每天批发x吨;
(2)在乙所列的方程中,代数式“$\frac{500}{x}$×(1+25%)”表示的意义是每天零售加批发的销量;
解决问题:设每天批发x吨,由题意得:
$\frac{500}{x}$-$\frac{500}{(1+25%)x}$=5,
解得:x=20,
经检验:x=20是原分式方程的解,
答:该合作社每天的批发量是20吨.
拓展反思:计划总利润(3000-1000)×500=1000000元;
实际总利润:500÷[20×(1+25%)]×20×(3000-1000)+(500-20×2)×(3500-1000)=1050000元;
利润增加:(1050000-1000000)÷1000000×100%=5%,
答:平均每吨的利润比原计划每吨的利润增加了5%.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意不要忘记检验.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
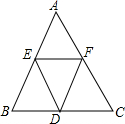 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
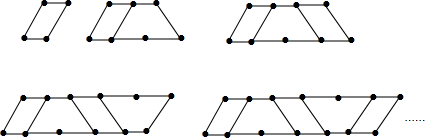
| A. | 5n+4 | B. | 5n+5 | C. | 4n+1 | D. | 4n+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com