
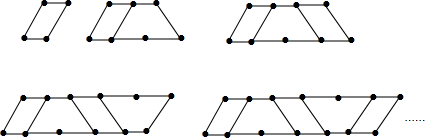
分析 由题意可知:第一个图形1个平行四边形需要4根火柴棒,第二个图形1个平行四边形、1个等腰梯形需要4+4=8根火柴棒,第三个图形2个平行四边形、1个等腰梯形需要4+4+3=11根火柴棒,第四个图形2个平行四边形、2个等腰梯形需要4+4+3+4=15根火柴棒,第五个图形3个平行四边形、2个等腰梯形需要4+4+3+4+3=18根火柴棒,…由此得出第奇数个图形,平行四边形$\frac{n+1}{2}$个,等腰梯形$\frac{n-1}{2}$个,需要1+3×$\frac{n+1}{2}$+4×$\frac{n-1}{2}$根火柴棒,得出第偶数个图形,平行四边形$\frac{n}{2}$个,等腰梯形$\frac{n}{2}$个,需要1+3×$\frac{n}{2}$+4×$\frac{n}{2}$根火柴棒,由此判定得出答案即可.
解答 解:∵第一个图形1个平行四边形需要4根火柴棒,
第二个图形1个平行四边形、1个等腰梯形需要4+4=8根火柴棒,
第三个图形2个平行四边形、1个等腰梯形需要4+4+3=11根火柴棒,第四个图形2个平行四边形、2个等腰梯形需要4+4+3+4=15根火柴棒,
第五个图形3个平行四边形、2个等腰梯形需要4+4+3+4+3=18根火柴棒,
…
∴第奇数个图形,平行四边形$\frac{n+1}{2}$个,等腰梯形$\frac{n-1}{2}$个,需要1+3×$\frac{n+1}{2}$+4×$\frac{n-1}{2}$根火柴棒,得出第偶数个图形,平行四边形$\frac{n}{2}$个,等腰梯形$\frac{n}{2}$个,需要1+3×$\frac{n}{2}$+4×$\frac{n}{2}$根火柴棒,
∵平行四边形、等腰梯形共11(6+5)个,
∴平行四边形6个,等腰梯形5个,需要1+3×6+4×5=39根火柴棒.
故答案为:39.
点评 此题考查图形的变化规律,找出图形蕴含的规律,得出数字之间的运算规律,利用规律解决问题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
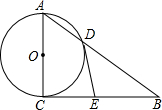 如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.
如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
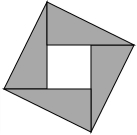 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是4.
如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15000名学生是总体 | |
| B. | 样本容量是1000名 | |
| C. | 每名学生是总体的一个样本 | |
| D. | 1000名学生的视力是总体的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com