
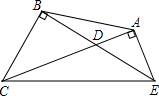
 如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB.
如图,△CDE中,∠CDE=135°,CB⊥DE于B,EA⊥CD于A,求证:CE=$\sqrt{2}$AB. 分析 取CE的中点F,连接AF、BF,根据直角三角形斜边上的中线等于斜边的一半可得AF=EF=BF=CF,根据三角形的内角和等于180°求出∠ACE+∠BEC=45°,然后求出∠AEC+∠BCE=135°,再根据等腰三角形两底角相等求出∠BFC+∠AFE=90°,然后求出∠AFB=90°,从而判断出△ABF是等腰直角三角形,然后根据等腰直角三角形的直角边等于斜边的$\frac{\sqrt{2}}{2}$可得AF=$\frac{\sqrt{2}}{2}$AB,然后证明即可.
解答 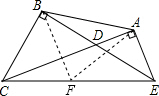 证明:如图,取CE的中点F,连接AF、BF,
证明:如图,取CE的中点F,连接AF、BF,
∵CB⊥DE,EA⊥CD,
∴AF=EF=BF=CF=$\frac{1}{2}$CE,
在△CDE中,∵∠CDE=135°,
∴∠ACE+∠BEC=180°-135°=45°,
∴∠AEC+∠BCE=(90°-∠ACE)+(90°-∠BEC)=180°-45°=135°,
∴∠BFC+∠AFE=(180°-2∠BCE)+(180°-2∠AEC)=360°-2(∠AEC+∠BCE)=360°-2×135°=90°,
∴∠AFB=180°-(∠BCF+∠AFE)=180°-90°=90°,
∴△ABF是等腰直角三角形,
∴AF=$\frac{\sqrt{2}}{2}$AB,
∴CE=2AF=2×$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$AB,
即CE=$\sqrt{2}$AB.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,等腰直角三角形的判定与性质,熟记各性质是解题的关键,作出图形更形象直观.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com