
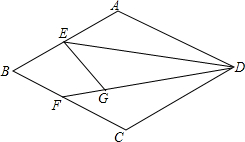
 如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$.
如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$. 分析 DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,根据菱形的性质得A=180°-∠B=120°,AB=AD=2,AD∥BC,则∠1=∠G,再利用折叠的性质得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,则∠4=60°,在Rt△EHG中利用含30度的直角三角形三边的关系得到HG=$\frac{1}{2}$EG=$\frac{1}{2}$,EH=$\sqrt{3}$EH=$\frac{\sqrt{3}}{2}$,则在Rt△DEH中利用勾股定理可计算出DE=$\sqrt{7}$,再证明∠2=∠G'得到FG'=FD,证明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后证明Rt△DEF∽Rt△DHE,利用相似比计算出DF=$\frac{14}{5}$,则FG=FD-DG=$\frac{4}{5}$,于是得到BF=FG=$\frac{4}{5}$.
解答 解DE和CB的延长线相交于G’点,连结EF,作EH⊥DF于H点,如图,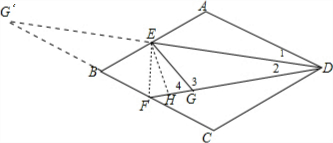
∵四边形ABCD为菱形,
∴∠A=180°-∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E为AB的中点,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
在Rt△EHG中,HG=$\frac{1}{2}$EG=$\frac{1}{2}$,EH=$\sqrt{3}$EH=$\frac{\sqrt{3}}{2}$,
在Rt△DEH中,DE=$\sqrt{E{H}^{2}+D{H}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+(2+\frac{1}{2})^{2}}$=$\sqrt{7}$,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG=FD,
在△AED和△BEG'中,
$\left\{\begin{array}{l}{∠1=∠G'}\\{∠AED=∠BEG'}\\{AE=BE}\end{array}\right.$,
∴△AED≌△BEG',
∴DE=G'E,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴$\frac{DF}{DE}$=$\frac{DE}{DH}$,即$\frac{DF}{\sqrt{7}}$=$\frac{\sqrt{7}}{\frac{5}{2}}$,
∴DF=$\frac{14}{5}$,
∴FG=FD-DG=$\frac{14}{5}$-2=$\frac{4}{5}$,
∴BF=FG=$\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了折叠的性质、全等三角形的判定与性质和相似三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | -1$\frac{1}{3}$ | B. | -|-$\frac{3}{4}$| | C. | -(-1$\frac{1}{3}$) | D. | |-$\frac{3}{4}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
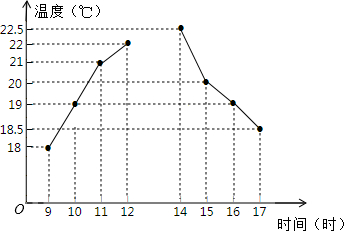 如图是小明根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图可知:该天下午(填上午或下午)的气温更稳定,理由是上午的方差大于下午的方差.
如图是小明根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图可知:该天下午(填上午或下午)的气温更稳定,理由是上午的方差大于下午的方差.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
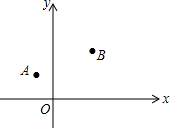 如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).
如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 100° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com