
 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 100° | C. | 45° | D. | 30° |
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
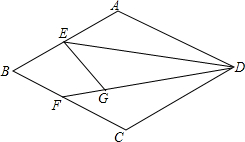 如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$.
如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
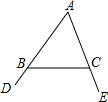 我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com