
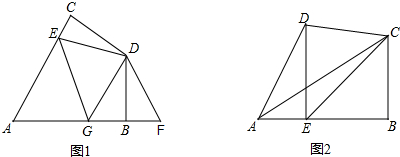
分析 (1)首先判断出∠C=∠DBF,然后根据全等三角形判定的方法,判断出△CDE≌△BDF,即可判断出DE=DF.
(2)猜想CE、EG、BG之间的数量关系为:CE+BG=EG.首先根据全等三角形判定的方法,判断出△ABD≌△ACD,即可判断出∠BDA=∠CDA=60°;然后根据∠EDG=60°,可得∠CDE=∠ADG,∠ADE=∠BDG,再根据∠CDE=∠BDF,判断出∠EDG=∠FDG,据此推得△DEG≌△DFG,所以EG=FG,最后根据CE=BF,判断出CE+BG=EG即可.
(3)根据(2)的证明过程,要使CE+BG=EG仍然成立,则∠EDG=∠BDA=∠CDA=$\frac{1}{2}$∠CDB,即∠EDG=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,据此解答即可.
(4)首先作CF⊥AD交AD的延长线于点F,根据全等三角形判定的方法,判断出△ACB≌△ACF,即可判断出AB=AF,CB=CF,推得BE+DF=DE;然后求出DE的值,判断出DF、BE的关系,即可求出BE的长是多少.
解答 (1)证明:
∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°-60°-120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在△CDE和△BDF中,
$\left\{\begin{array}{l}{CD=BD}\\{∠C=∠DBF}\\{CE=BF}\end{array}\right.$(SAS)
∴△CDE≌△BDF,
∴DE=DF.
(2)解:如图1,连接AD, ,
,
猜想CE、EG、BG之间的数量关系为:CE+BG=EG.
证明:在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$(SSS)
∴△ABD≌△ACD,
∴∠BDA=∠CDA=$\frac{1}{2}∠CDB$=$\frac{1}{2}×120°$=60°,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得
△CDE≌△BDF,
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在△DEG和△DFG中,
$\left\{\begin{array}{l}{DE=DF}\\{∠EDG=∠FDG}\\{DG=DG}\end{array}\right.$
∴△DEG≌△DFG,
∴EG=FG,
又∵CE=BF,FG=BF+BG,
∴CE+BG=EG.
(3)解:要使CE+BG=EG仍然成立,
则∠EDG=∠BDA=∠CDA=$\frac{1}{2}$∠CDB,
即∠EDG=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∴当∠EDG=90°-$\frac{1}{2}$α时,CE+BG=EG仍然成立.
(4)解:如图2,作CF⊥AD交AD的延长线于点F,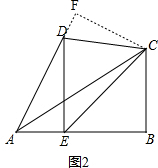 ,
,
在△ACB和△ACF中,
$\left\{\begin{array}{l}{∠CAB=∠CAF=30°}\\{∠CBA=∠CFA=90°}\\{AC=AC}\end{array}\right.$(AAS)
∴△ACB≌△ACF,
∴AB=AF,CB=CF,
∴由(2),可得
BE+DF=DE,
∵DE⊥AB,
∴∠AED=90°,
又∵∠CAB=∠CAD=30°,
∴∠EAD=30°+30°=60°,∠ADE=30°,
∴AD=2AE=2×3=6,DE=$\sqrt{3}AE$=3$\sqrt{3}$,
∵AD+DF=AE+BE,
∴6+DF=3+BE,
∴DF=BE-3,
又∵BE+DF=DE,
∴2BE-3=3$\sqrt{3}$,
∴BE=$\frac{3+3\sqrt{3}}{2}$.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -1$\frac{1}{3}$ | B. | -|-$\frac{3}{4}$| | C. | -(-1$\frac{1}{3}$) | D. | |-$\frac{3}{4}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
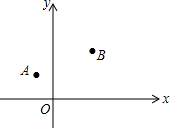 如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).
如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
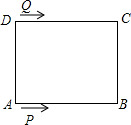 如图,长方形ABCD中,AB=CD=10cm,BC=AD=8侧面,动点P从点A出发,沿A→B→C→D路线运动到D停止,动点Q从点D出发,沿D→C→B→A路线运动到A停止.若P、Q同时出发,点P速度为2cm/s,点Q速度为1cm/s,6s后点Q改变速度为2cm/s,点P速度不变.
如图,长方形ABCD中,AB=CD=10cm,BC=AD=8侧面,动点P从点A出发,沿A→B→C→D路线运动到D停止,动点Q从点D出发,沿D→C→B→A路线运动到A停止.若P、Q同时出发,点P速度为2cm/s,点Q速度为1cm/s,6s后点Q改变速度为2cm/s,点P速度不变.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 100° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com