
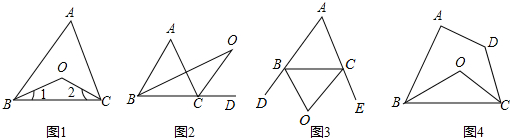
分析 (1)根据角平分线的定义可得∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠2=$\frac{1}{2}$∠ACD=$\frac{1}{2}$(∠A+∠ABC),∠BOC=∠2-∠1,然后整理即可得解;
(2)根据三角形的外角性质以及角平分线的定义表示出∠OBC和∠OCB,再根据三角形的内角和定理解答;
(3)同(1)的求解思路;
解答 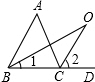 解:(1)探究2结论:∠BOC=$\frac{1}{2}$∠A.
解:(1)探究2结论:∠BOC=$\frac{1}{2}$∠A.
理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠2=$\frac{1}{2}$∠ACD=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠1,
∵∠2是△BOC的一个外角,
∴∠BOC=∠2-∠1=$\frac{1}{2}$∠A+∠1-∠1=$\frac{1}{2}$∠A,
即∠BOC=$\frac{1}{2}$∠A;
(2)由三角形的外角性质和角平分线的定义,∠OBC=$\frac{1}{2}$(∠A+∠ACB),∠OCB=$\frac{1}{2}$(∠A+∠ABC),
在△BOC中,∠BOC=180°-∠OBC-∠OCB=180°-$\frac{1}{2}$(∠A+∠ACB)-$\frac{1}{2}$(∠A+∠ABC),
=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC),
=180°-$\frac{1}{2}$(180°+∠A),
=90°-$\frac{1}{2}$∠A;
(3)∠OBC+∠OCB=$\frac{1}{2}$(360°-∠A-∠D),
在△BOC中,∠BOC=180°-$\frac{1}{2}$(360°-∠A-∠B)=$\frac{1}{2}$(∠A+∠D).
点评 本题考查了三角形的外角性质,角平分线的定义,三角形的内角和定理,熟记性质并准确识图,整体思想的利用是解题的关键.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
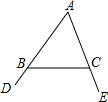 我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
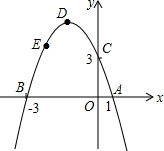 若抛物线的顶点为点D(-1,4),点E(-2,n)在抛物线上,x轴,y轴上是否存在点P,Q,使四边形PQDE的周长最小?若存在,求出最小值;若不存在,请说明理由.
若抛物线的顶点为点D(-1,4),点E(-2,n)在抛物线上,x轴,y轴上是否存在点P,Q,使四边形PQDE的周长最小?若存在,求出最小值;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com