
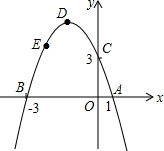
 若抛物线的顶点为点D(-1,4),点E(-2,n)在抛物线上,x轴,y轴上是否存在点P,Q,使四边形PQDE的周长最小?若存在,求出最小值;若不存在,请说明理由.
若抛物线的顶点为点D(-1,4),点E(-2,n)在抛物线上,x轴,y轴上是否存在点P,Q,使四边形PQDE的周长最小?若存在,求出最小值;若不存在,请说明理由. 分析 先求得抛物线的解析式,然后可求得点E的坐标,接下来,作出点D关于y轴的对称点D′,点E关于x轴的对称点E′,四边形的周长等于D′E′和ED的长度之和.
解答 解:存在.
理由:设抛物线的解析式为y=a(x+1)2+4,将x=1,y=0代入得:a=-1.
∴抛物线的解析式为y=-(x+1)2+4,
将x=-2代入得:n=3,
∴点E的坐标为(-2,3).
作出点D关于y轴的对称点D′,点E关于x轴的对称点E′,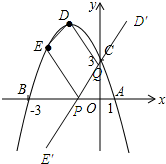
∴点D′的坐标(1,4),点E′的坐标为(-2,-3)
连接D′E′交x、y轴与点P,Q.
根据两点之间的距离公式可知:D′E′=$\sqrt{[1-(-2)]^{2}+[4-(-3)]^{2}}$=$\sqrt{58}$,
DE=$\sqrt{[-1-(-2)]^{2}+(4-3)^{2}}$=$\sqrt{2}$.
由轴对称的性质可知:DQ=D′Q,EP=E′P,
∴四边形的周长=ED+EP+PQ+DQ=ED+E′P+PQ+QD′=$\sqrt{58}+\sqrt{2}$.
点评 本题主要考查的是二次函数图象上点的坐标特点,轴对称的性质,两点间的距离公式的应用,由两点之间线段得出点D′、Q、P、E′在一条直线上时,四边形的周长有最小值是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )| A. | 800 | B. | 600 | C. | 400 | D. | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
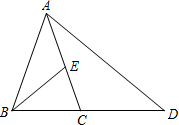 已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.
已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、D、E在⊙O上,点B、C在AD上,BC=2,△BCE为等边三角形,且∠AOD=120°.
如图,点A、D、E在⊙O上,点B、C在AD上,BC=2,△BCE为等边三角形,且∠AOD=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com