练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．某校随机抽取200名学生，对他们喜欢的图书类型进行问卷调查，统计结果如图．根据图中信息，估计该校2000名学生中喜欢文学类书籍的人数是（　　）
    A．800B．600C．400D．200

    分析 利用扇形统计图得到样本中喜欢文学类书籍的人数的百分比为40%，用它表示该校2000名学生中喜欢文学类书籍的人数的百分比，从而可估算出全校喜欢文学类书籍的人数．

    解答 解：2000×40%=800（人）．
    估计该校2000名学生中喜欢文学类书籍的人数为800人．
    故选A．

    点评 本题考查了用样本估计总体：用样本估计总体是统计的基本思想．用样本的数字特征估计总体的数字特征（主要数据有众数、中位数、平均数、标准差与方差 ）．一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，在△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A=55°，∠BDC=95°，求△BDE各内角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知：△ABC中，AB=4，AC=3，BC=$\sqrt{7}$，则△ABC的面积是$\frac{3}{2}$$\sqrt{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

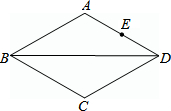    18．如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（　　）
    A．2B．4C．$\sqrt{3}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．阅读下面材料：
    小明遇到这样一个问题：如图1，在△ABC中，D为BC中点，E、F分别为AB、AC上一点，且ED⊥DF，求证：BE+CF＞EF．
    小明发现，延长FD到点H，使DH=FD，连结BH、EH，构造△BDH和△EFH，通过证明△BDH与△CDF全等、△EFH为等腰三角形，利用△BEH使问题得以解决（如图2）．
    参考小明思考问题的方法，解决问题：
    如图3，在矩形ABCD中，O为对角线AC中点，将矩形ABCD翻折，使点B恰好与点O重合，EF为折痕，猜想EF、AE、FC之间的数量关系？并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知a，b都是有理数，且2a+3$\sqrt{5}$b=b-$\sqrt{5}$a-$\sqrt{5}$，则a=-$\frac{1}{7}$，b=-$\frac{2}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

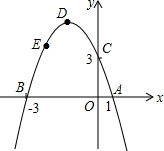    2．若抛物线的顶点为点D（-1，4），点E（-2，n）在抛物线上，x轴，y轴上是否存在点P，Q，使四边形PQDE的周长最小？若存在，求出最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

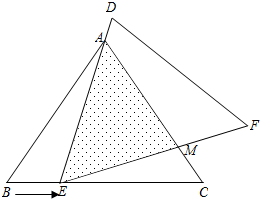    6．如图，在△ABC中，己知AB=AC=5，BC=6，且将△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．
    （1）求证：△ABE∽△ECM；
    （2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；
    （3）当点E运动到什么位置时，线段AM最短？并求出此时AM的值．（直接写出答案）

    查看答案和解析>>

    同步练习册答案