
分析 由于a,b都是有理数,比较等式左右两边的有理数部分和无理数部分,可得a、b的值.
解答 解:原式可化为2a+3$\sqrt{5}$b=b-$\sqrt{5}$(a+1),
∵a,b都是有理数,
∴$\left\{\begin{array}{l}2a=b\\ a+1=-3b\end{array}\right.$,解得$\left\{\begin{array}{l}a=-\frac{1}{7}\\ b=-\frac{2}{7}\end{array}\right.$.
故答案为:-$\frac{1}{7}$,-$\frac{2}{7}$.
点评 本题考查的是二次根式的加减法,熟知有理数、无理数的定义及它们之间的关系是解答此题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
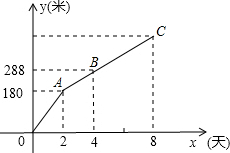 如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长.
如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )| A. | 800 | B. | 600 | C. | 400 | D. | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com