
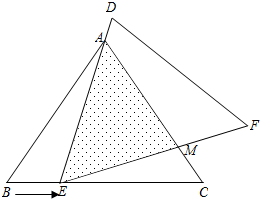
 如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.分析 (1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证得∠CEM=∠BAE,则可证得:△ABE∽△ECM;
(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案;
(3)先设BE=x,由△ABE∽△ECM,根据相似三角形的对应边成比例,易得CM=-$\frac{1}{5}$(x-3)2+$\frac{9}{5}$,利用二次函数的性质,继而求得线段AM的最小值.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC-EC=6-5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴$\frac{CE}{AC}=\frac{AC}{BC}$,
∴CE=$\frac{A{C}^{2}}{CB}$=$\frac{25}{6}$,
∴BE=6-$\frac{25}{6}$=$\frac{11}{6}$;
∴BE=1或$\frac{11}{6}$;
(3)解:设BE=x,
又∵△ABE∽△ECM,
∴$\frac{CM}{BE}$=$\frac{CE}{AB}$,
即:$\frac{CM}{x}$=$\frac{6-x}{5}$,
∴CM=-$\frac{{x}^{2}}{5}$+$\frac{6}{5}$x=-$\frac{1}{5}$(x-3)2+$\frac{9}{5}$,
∴AM=-5-CM=$\frac{1}{5}$(x-3)2+$\frac{16}{5}$,
∴当x=3时,AM最短为$\frac{16}{5}$,
∴BE=3时,AM最短为$\frac{16}{5}$.
点评 此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及二次函数的最值问题.此题难度较大,注意数形结合思想、分类讨论思想与函数思想的应用是解此题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:选择题
 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )| A. | 800 | B. | 600 | C. | 400 | D. | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
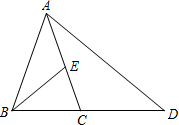 已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.
已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p=9,q=3 | B. | p=9,q=-3 | C. | p=-9,q=3 | D. | p=-9,q=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com