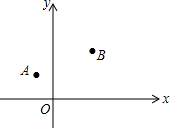Question

13．如图所示，x轴所在直线是一条东西走向的河，A（-2，3）、B（4，5）两个村庄位于河的北岸，现准备在河上修建一净水站P，并利用管道为两个村庄供水（单位：千米）．
（1）欲使所修管道最短，应该把净水站P修在什么位置，作出正确图形（用尺规作图），求出P点坐标及PB所在直线解析式；
（2）若管道每米费用需要200元，求修管道的最低费用．

Answer 1

分析 （1）作点A关于x轴的对称点A′，连接A′B交x轴于P，则点P即为所求；根据关于x轴对称的点的坐标特征得到A′（-2，-3），根据待定系数法即可得到结果；
（2）根据题意A′B即为所修管道的长，分别过A′，B作平行于x轴和y轴的直线交于点B′，根据勾股定理即可得到结论．

解答 解：（1）作点A关于x轴的对称点A′，连接A′B交x轴于P，则点P即为所求；
∵A（-2，3），
∴A′（-2，-3），
设直线PB的解析式为：y=kx+b，∵直线PB过A′（-2，-3），B（4，5），
∴$\left\{\begin{array}{l}{-3k+b=-3}\\{4k+b=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$．
∴直线PB的解析式为：y=$\frac{4}{3}$x-$\frac{1}{3}$，

（2）根据题意A′B即为所修管道的长，分别过A′，B作平行于x轴和y轴的直线交于点B′，
在直角三角形A′B′B中，A′B′=6，B′B=8，
∴A′B=10，
∴修管道的最低费用=200×10×100=2×10⁶元．

点评 本题考查了轴对称-最短距离问题，用待定系数法确定函数的解析式的方法求解．两点之间线段最短是解题的关键．