
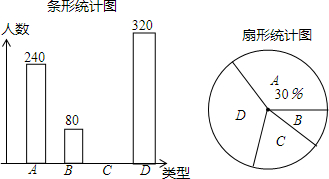
分析 (1)先求出调查的人数,再求出这个社区的居民总人数,
(2)先求出喜欢吃C种粽子的人数,再求出喜欢吃C种粽子对应扇形的圆心角的度数,补全条形统计图即可,
(3)利用全市爱吃C种粽子的人数=全市总人数×爱吃C种粽子的百分比.
解答 解:(1)调查这个社区的居民人数为240÷30%=800(人),
这个社区的居民总人数为:800÷10%=8000(人);
(2)喜欢吃C种粽子的人数为800-240-80-320=160(人),
喜欢吃C种粽子对应扇形的圆心角的度数是$\frac{160}{800}$×360°=72°
补全条形统计图,
故答案为:72°.
(3)爱吃C种粽子的人数为20×$\frac{160}{800}$=4(万人).
点评 本题主要考查了条形统计图与扇形统计图,解题的关键是读懂统计图,从统计图中获得准确的信息.


科目:初中数学 来源: 题型:解答题
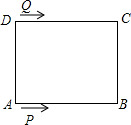 如图,长方形ABCD中,AB=CD=10cm,BC=AD=8侧面,动点P从点A出发,沿A→B→C→D路线运动到D停止,动点Q从点D出发,沿D→C→B→A路线运动到A停止.若P、Q同时出发,点P速度为2cm/s,点Q速度为1cm/s,6s后点Q改变速度为2cm/s,点P速度不变.
如图,长方形ABCD中,AB=CD=10cm,BC=AD=8侧面,动点P从点A出发,沿A→B→C→D路线运动到D停止,动点Q从点D出发,沿D→C→B→A路线运动到A停止.若P、Q同时出发,点P速度为2cm/s,点Q速度为1cm/s,6s后点Q改变速度为2cm/s,点P速度不变.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 100° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
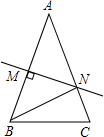 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
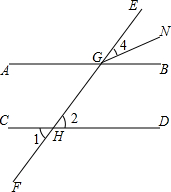 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com