
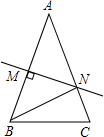
 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 根据等腰三角形的性质求出∠ABC和∠ACB的度数,根据线段垂直平分线的性质证明NB=NA,进行判断即可.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵MN是AB的垂直平分线,
∴NB=NA,∴∠NBA=∠A=36°,
∴∠NBC=∠ABC-∠NBC=36°,
∴BN平分∠ABC,①正确;
∠BNC=∠A+∠NBC=72°,
∴∠BNC=∠ACB,
∴△BCN是等腰三角形,②正确;
△BMN是直角三角形,△BCN是锐角三角形,∴△BMN≌△BCN不正确,③错误;
△BCN的周长等于BN+CN+BC=AN+CN+BC=AC+BC=AB+BC,④正确,
故选:B.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
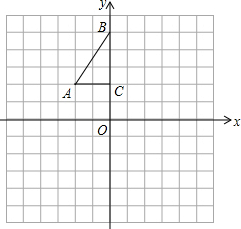 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
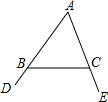 我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
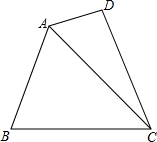 如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.
如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com