练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．若（a-2b+3c+4）2+（2a-3b+4c-5）2≤0，则6a-10b+14c-3的值为-1．

    分析 利用非负数的性质列出方程组，整理求出3a-5b+7c的值，代入原式计算即可求出值．

    解答 解：∵（a-2b+3c+4）2+（2a-3b+4c-5）2≤0，
    ∴$\left\{\begin{array}{l}{a-2b+3c=-4①}\\{2a-3b+4c=5②}\end{array}\right.$，
    ①+②得：3a-5b+7c=1，
    则原式=2（3a-5b+7c）-3=2-3=-1，
    故答案为：-1

    点评 此题考查了解三元一次方程组，以及非负数的性质，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．下列关于概率的描述属于“等可能性事件”的是（　　）
    A．交通信号灯有“红、绿、黄”三种颜色，它们发生的概率
    B．掷一枚图钉，落地后钉尖“朝上”或“朝下”的概率
    C．小亮在沿着“直角三角形”三边的小路上散步，他出现在各边上的概率
    D．小明用随机抽签的方式选择以上三种答案，则A、B、C被选中的概率

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列说法正确的是（　　）
    A．对角线互相垂直的四边形是菱形
    B．两条对角线互相垂直平分的四边形是正方形
    C．对角线互相垂直的四边形是平行四边形
    D．对角线相等且互相平分的四边形是矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：如图∥AD，∠1=∠2，∠BAC=60°，求∠AGD的度数．
    请你根据已知调进补充推理过程，并在相应括号内注明理由．
    解：∵EF∥AD（已知），
    ∴∠2=∠3（两直线平行，同位角相等）．
    又∵∠1=∠2（已知），
    ∴∠1=∠3（等量代换），
    ∴AB∥DG（内错角相等，两直线平行）
    ∴∠BAC+∠DGC=180°（两直线平行，同位角相等）
    而∠BAC=60°，∴∠AGD=120°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．汽车开始行使时，油箱中有油55升，如果每小时耗油7升，则油箱内剩余油量y（升）与行使时间t（小时）的关系式为y=-7t+55．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

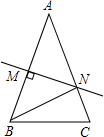    18．如图，在三角形ABC中，AB=AC，∠A=36°，AB的垂直平分线MN交AB于点M，交AC于点N，下面结论：①BN平分∠ABC；②△BCN是等腰三角形；③△BMN≌△BCN；④△BCN的周长等于AB+BC，其中正确的结论是（　　）
    A．①②③B．①②④C．②③④D．①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

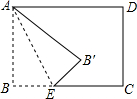    5．如图，将长方形ABCD沿直线AE折叠，点B落在点B′处，已知BC=8，AB=6，若△B′EC为直角三角形，则BE的长为3或6或$\frac{25}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列各数中，是无理数的是（　　）
    A．$\frac{22}{7}$B．0.101001C．$\sqrt{81}$D．$\sqrt{32}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：$\sqrt{16}÷\sqrt{2}-\sqrt{3}×（2-\sqrt{3}）-\frac{3}{2}\sqrt{（-2）^{2}}$-$|1-\sqrt{2}|+\sqrt{\frac{1}{2}}-（1-\sqrt{3}）^{2}$．

    查看答案和解析>>

    同步练习册答案