
【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元) | 投放数量 (单位:辆) | 总价(单位:元) | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计(单位:元) | 7500 | ||
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.

【答案】问题1:100;50(x+10);问题2:A、B两型自行车的单价分别是70元和80元;问题3:甲街区每100人投放A型“小黄车”2辆.
【解析】
问题1:看图填数即可;
问题2:设A型车的成本单价为x元,则B型车的成本单价为(x+10)元,根据成本共计7500元,列方程求解即可;
问题3:根据两个街区共有![]() 人,列出分式方程进行求解并检验即可.
人,列出分式方程进行求解并检验即可.
解:问题1:50+50=100(辆)
∴本次试点投放的A、B型“小黄车”共有 100辆;
B型自行车的成本总价为:50(x+10)
故答案为:100;50(x+10)
问题2:设A型车的成本单价为x元,B型车的成本单价为(x+10)元,依题意得
50x+50(x+10)=7500,
解得x=70,
∴x+10=80,
答:A、B两型自行车的单价分别是70元和80元;
问题3:![]() ,
,
解得:n=2
经检验:n=2是所列方程的解,
∴甲街区每100人投放A型“小黄车”2辆.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.∠1=∠3,求证:AB∥DC.
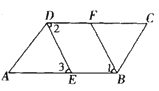
证明:∵∠ABC=∠ADC ( )
∴![]() ( )
( )
∵BF、DE分别平分∠ABC与∠ADC ( )
∴![]() ( )
( )
∴∠______=∠______ ( )
∵∠1=∠3( )
∴∠2=∠______ (等量代换)
∴____∥____ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的点P,Q,给出如下定义:若点P到点Q的距离为d(d≥0),则称d为点P到点Q的d追随值,记作d[PQ].例如,在数轴上点P表示的数是2,点Q表示的数是5,则点P到点Q的d追随值为d[PQ]=3.
问题解决:
(1)点M,N都在数轴上,点M表示的数是1,且点N到点M的d追随值d[MN]=a(a≥0),则点N表示的数是_____(用含a的代数式表示);
(2)如图,点C表示的数是1,在数轴上有两个动点A,B都沿着正方向同时移动,其中A点的速度为每秒3个单位,B点的速度为每秒1个单位,点A从点C出发,点B表示的数是b,设运动时间为t(t>0).
①当b=4时,问t为何值时,点A到点B的d追随值d[AB]=2;
②若0<t≤3时,点A到点B的d追随值d[AB]≤6,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
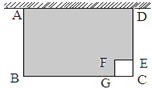
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com