
【题目】如图,已知动点A在反比例函数y=![]() (x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
(x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
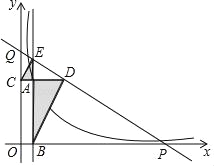
【答案】10
【解析】
作DM⊥OP于M,EN⊥OQ于N,设点A(a,b),则ab=6,由△ACE∽△ADB,得AD=![]() b,由△QNE∽△DMP,得QN=
b,由△QNE∽△DMP,得QN=![]() b,MP=9a,由△EAD∽△DMP,得
b,MP=9a,由△EAD∽△DMP,得![]() ,即
,即![]() ,所以b=6a,解得a=1,b=6,即可求得阴影部分的面积.
,所以b=6a,解得a=1,b=6,即可求得阴影部分的面积.
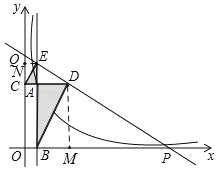
解:如图,作DM⊥OP于M,EN⊥OQ于N,
设点A(a,b),
∵点A在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴ab=6,
∵CE∥BD且CA:AE=1:2,
∴△ACE∽△ADB,
∴![]() ,
,
∴AD=![]() b,
b,
∵NE∥OP,
∴∠QEN=∠DPM,
∵∠QNE=∠DMP=90°,
△QNE∽△DMP,
∴![]() ,
,
∴QN=![]() b,MP=9a,
b,MP=9a,
∵CD∥x轴,EB∥y轴,
∴△EAD∽△DMP,
∴![]() ,即
,即![]() ,
,
∴b=6a,
∴a=1,b=6,
∴阴影部分的面积=![]() .
.
故答案为:10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
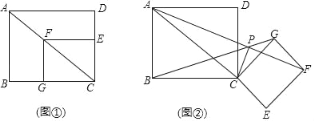
【题目】如图①,四边形ABCD与四边形CEFG都是矩形,点E,G分别在边CD,CB上,点F在AC上,AB=3,BC=4
(1)求![]() 的值;
的值;
(2)把矩形CEFG绕点C顺时针旋转到图②的位置,P为AF,BG的交点,连接CP
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断CP与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,直线与圆有三种位置关系:相交、相切、相离.类比直线与圆的位置关系,给出如下定义:与坐标轴不平行的直线与抛物线有两个公共点叫做直线与抛物线相交;直线与抛物线有唯一的公共点叫做直线与抛物线相切,这个公共点叫做切点;直线与抛物线没有公共点叫做直线与抛物线相离.
(1)记一次函数![]() 的图像为直线
的图像为直线![]() ,二次函数
,二次函数![]() 的图像为抛物线
的图像为抛物线![]() ,若直线
,若直线![]() 与抛物线
与抛物线![]() 相交,求
相交,求![]() 的取值范围;
的取值范围;
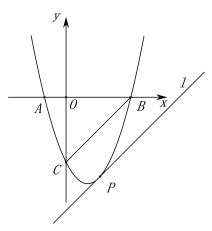
(2)若二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线l与CB平行,并且与该二次函数的图像相切,求切点P的坐标.
,直线l与CB平行,并且与该二次函数的图像相切,求切点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
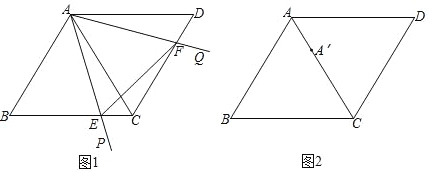
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
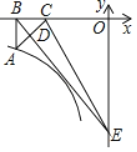
【题目】如图点A在反比例函数y=![]() (x<0)的图象上,作Rt△ABC,直角边BC在x轴上,点D为斜边AC的中点,直线BD交y轴于点E,若△BCE的面积为8,则k=_____.
(x<0)的图象上,作Rt△ABC,直角边BC在x轴上,点D为斜边AC的中点,直线BD交y轴于点E,若△BCE的面积为8,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com