
如图,在△ABC 中,AB=AC,DE 垂直平分 AB,分别交 AB、AC 于点 D、E,若∠EBC=30°, 则∠A=( )
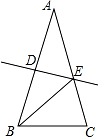
A.30° B.35° C.40° D.45°
C【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】设∠A 为 x,根据线段的垂直平分线的性质得到 EA=EB,用 x 表示出∠BEC,根据等腰三 角形的性质得到∠ABC=∠C,根据三角形内角和定理列出方程,解方程即可.
【解答】解:设∠A 为 x,
∵DE 垂直平分 AB,
∴EA=EB,
∴∠EBA=∠A=x,
∴∠BEC=2x,
∵AB=AC,
∴∠ABC=∠C,
∴30°+x+30°+2x=180°,
解得,x=40°, 故选:C.
【点评】此题主要考查线段的垂直平分线的性质和三角形内角和定理的应用,掌握线段的垂直平分 线上的点到线段的两个端点的距离相等是解题的关键.


科目:初中数学 来源: 题型:
如图,DE⊥AB 于 E,DF⊥AC 于 F,若 BD=CD、BE=CF.
(1)求证:AD 平分∠BAC;
直接写出 AB+AC 与 AE 之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
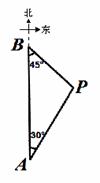
如图,A、B两座城市相距100千米,现计划在两城市间修筑一条
高速公路(即线段AB).经测量,森林保护区中心P点既在A城市
的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森
林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:
计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.
(参考数据: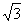 ≈1.732,
≈1.732,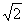 ≈1.414)
≈1.414)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com