
【题目】如图,已知![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 表示的数为3,
表示的数为3,![]() ,
,![]() 。
。
![]()
(1)数轴上点![]() 表示的数为,点
表示的数为,点![]() 表示的数为。
表示的数为。
(2)动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 以每秒2个单位长度的速度沿数轴向右匀速运动,点
以每秒2个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒1个单位长度的速度沿数轴向左匀速运动,
以每秒1个单位长度的速度沿数轴向左匀速运动,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,设运动时间为
,设运动时间为![]() (
(![]() )秒。
)秒。
①求数轴上![]() 、
、![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,原点
为何值时,原点![]() 恰好是线段
恰好是线段![]() 的中点;
的中点;
【答案】(1)-5,1;(2)①M表示的数是-5+t;N表示的数是3-![]() t;②当t=2秒时,O为PQ的中点.
t;②当t=2秒时,O为PQ的中点.
【解析】
(1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=![]() CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②此题有两种情况:当点P在点O的左侧,点Q在点O的右侧时;当P在点O的右侧,点Q在点O的左侧时,分别画出图形进行计算即可.
解:(1)∵C表示的数为3,BC=2,
∴OB=3-2=1,
∴B点表示1.
∵AB=6,
∴AO=6-1=5,
∴A点表示-5;
(2)①由题意得:AP=2t,CQ=t,如图1所示:
,
∴AM=![]() ,AM=t,
,AM=t,
∴在数轴上点M表示的数是-5+t,,
∵点N在CQ上,CN=![]() CQ,∴CN=
CQ,∴CN=![]() t,
t,
∴在数轴上点N表示的数是3-![]() t;
t;
②如图2所示:由题意得,AP=3t,CQ=t,分两种情况:
i)当点P在点O的左侧,点Q在点O的右侧时,OP=5-2t,OQ=3-t,
![]()
∵O为PQ的中点,
∴OP=OQ,
∴5-2t=3-t,
解得:t=2,当t=2秒时,O为PQ的中点;
ii)当P在点O的右侧,点Q在点O的左侧时,OP=2t-5,OQ=t-3,
![]()
∵O为PQ的中点,
∴OP=OQ,
∴2t-5=t-3,解得:t=2,此时0P=-1<0,线段不能为负,舍去,
综上所述:当t=2秒时,O为PQ的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
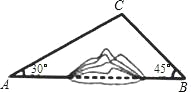
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(+17)+(-12);
(2)10+(―![]() )―6―(―0.25);
)―6―(―0.25);
(3)(![]() )×48 ;
)×48 ;
(4)|-5-4|-5×(-2)2-1÷(-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥BD,折线AMB夹在两条平行线间.(1)判断∠M,∠A,∠B的关系;(2)请你尝试改变问题中的某些条件,探索相应的结论.建议:①折线中折线段数量增加到n条(n=3,4,…);
②可如图1,图2,或M点在平行线外侧.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为45平方米的花圃,那么AB的长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() ________时,四边形
________时,四边形![]() 是正方形
是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com