
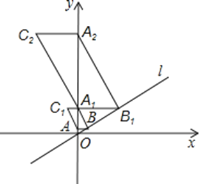
【题目】如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作□ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作□A1B1A2C2;…;按此作法继续下去,则C3的坐标是 ____________;Cn的坐标是 _____________________
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成。已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.

(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围.
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
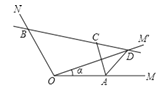
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,则有:(1)AD=__ CD(填数量关系);(2)△ACD面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过实验获得两个变量 x(x 0), y( y 0) 的一组对应值如下表。
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 7 | 3.5 | 2.33 | 1.75 | 1.4 | 1.17 | 1 |
(1)在网格中建立平面直角坐标系,画出相应的函数图象,求出这个函数表达式;
(2)结合函数图象解决问题:(结果保留一位小数)

①![]() 的值约为多少?
的值约为多少?
②点A坐标为(6,0),点B在函数图象上,OA=OB,则点B的横坐标约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com