
【题目】如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,![]() ≈1.732)
≈1.732)
【答案】解:如图,过M作MN⊥AC交于N点,即MN最短,
∵∠EAD=60°,∠CAD=30°,
∴∠CAM=30°,
∴∠AMN=60°,
又∵C处看M点为北偏西60°,
∴∠FCM=60°,
∴∠MCB=30°,
∵∠EAC=60°,
∴∠CAD=30°,
∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,
∴在Rt△AMC中,∠AMC=90°,∠MAC=30°,
∴MC=![]() AC=2000,∠CMN=30°,
AC=2000,∠CMN=30°,
∴NC=![]() MC=1000,
MC=1000,
∵AC=4000米,
∴AN=AC﹣NC=4000﹣1000=3000(米).
答:点N到A市最短路线3000米.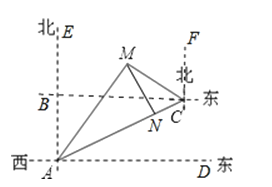
【解析】过M作MN⊥AC交于N点,即MN最短,根据方向角可以证得∠AMC=90°,根据三角函数即可求得MC,进而求得AN的长.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】暑假里某班同学相约一起去某公园划船,在售票处了解到该公园划船项目收费标准如下:
船型 | 两人船(仅限两人) | 四人船(仅限四人) | 六人船(仅限六人) | 八人船(仅限八人) |
每船租金(元/小时) |
| 100 | 130 |
|
(1)其中,两人船项目和八人船项目单价模糊不清,通过询问,了解到以下信息:
①一只八人船每小时的租金比一只两人船每小时的租金的2倍少30元;
②租2只两人船,3只八人船,游玩一个小时,共需花费630元.
请根据以上信息,求出两人船项目和八人船项目每小时的租金;
(2)若该班本次共有18名同学一起来游玩,每人乘船的时间均为 1小时,且每只船均坐满,试列举出可行的方案(至少四种),通过观察和比较,找到所有方案中最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为 cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).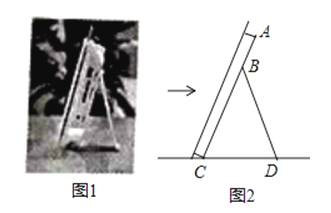
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10![]() 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点D,E分别在AB,AC上,EF交BC于点F,DG交BC于点G,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.
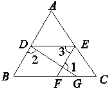
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)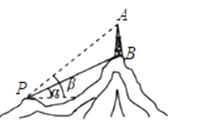
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮 | 第2轮 | 第3轮 | 第4轮 | 第5轮 | 第6轮 | |
甲 | 10 | 14 | 12 | 18 | 16 | 20 |
乙 | 12 | 11 | 9 | 14 | 22 | 16 |
下列说法不正确的是( )
A.甲得分的极差小于乙得分的极差
B.甲得分的中位数大于乙得分的中位数
C.甲得分的平均数大于乙得分的平均数
D.乙的成绩比甲的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2 , 线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.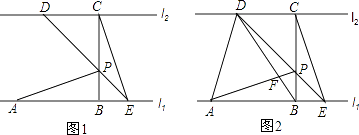
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当 ![]() =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当 ![]() =n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求
=n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com