Question

【题目】如图，已知直线l1∥l2 ， 线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．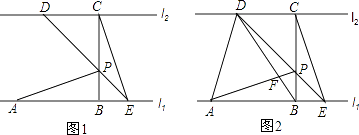

（1）求证：△ABP≌△CBE；
（2）连结AD、BD，BD与AP相交于点F．如图2．
①当 =2时，求证：AP⊥BD；
②当 =n（n＞1）时，设△PAD的面积为S1 ， △PCE的面积为S2 ， 求 的值．

Answer 1

【答案】
（1）

证明：∵BC⊥直线l1，

∴∠ABP=∠CBE，

在△ABP和△CBE中

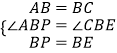
∴△ABP≌△CBE（SAS）

（2）

①证明：连结BD，延长AP交CE于点H，

∵△ABP≌△CBE，

∴∠APB=∠CEB，

∵∠PAB+∠APB=90°，

∴∠PAB+∠CEB=90°，

∴AH⊥CE，

∵ =2，即P为BC的中点，直线l1∥直线l2，

∴△CPD∽△BPE，

∴ ，

∴DP=PE，

∴四边形BDCE是平行四边形，

∴CE∥BD，

∵AH⊥CE，

∴AP⊥BD；

②解：∵ =n，

∴BC=nBP，

∴CP=（n﹣1）BP，

∵CD∥BE，

易得△CPD∽△BPE，

∴ =n﹣1，

设△PBE的面积S△PBE=S，则△PCE的面积S△PCE满足 =n﹣1，

即S2=（n﹣1）S，

∵S△PAB=S△BCE=nS，

∴S△PAE=（n+1）S，

∵ = =n﹣1，

∴S1=（n﹣1）S△PAE，即S1=（n+1）（n﹣1）S，

∴ = =n+1．

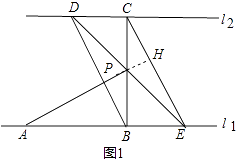
【解析】（1）求出∠ABP=∠CBE，根据SAS推出即可；（2）①延长AP交CE于点H，求出AP⊥CE，证出△CPD∽△BPE，推出DP=PE，求出平行四边形BDCE，推出CE∥BD即可；②分别用S表示出△PAD和△PCE的面积，代入求出即可．
【考点精析】认真审题，首先需要了解相似三角形的性质(对应角相等，对应边成比例的两个三角形叫做相似三角形)．