练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．计算：
    （1）2a6b3÷a3b2        
    （2）-12x3y4z2÷（-4x2y2z）         
    （3）-$\frac{1}{4}$a6b4c÷2a3c
    （4）6x2ny÷3xny       
    （5）（-2r2s）2÷4rs2．

    分析 （1）直接利用单项式除以单项式运算法则化简求出答案；
    （2）直接利用单项式除以单项式运算法则化简求出答案；
    （3）直接利用单项式除以单项式运算法则化简求出答案；
    （4）直接利用单项式除以单项式运算法则化简求出答案；
    （5）直接利用积的乘方运算法则化简，再利用单项式除以单项式运算法则化简求出答案．

    解答 解：（1）2a6b3÷a3b2=2a3b；

    （2）-12x3y4z2÷（-4x2y2z）=3xy2z；

    （3）-$\frac{1}{4}$a6b4c÷2a3c=-$\frac{1}{8}$a3b4；

    （4）6x2ny÷3xny=3xn；

    （5）（-2r2s）2÷4rs2=4r4s2÷4rs2=r3．

    点评 此题主要考查了整式的乘除运算，正确掌握运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．如图，正方形ABCD位于第一象限，边长为3，点A在直线y=x上，点A的横坐标为1，正方形ABCD的边分别平行于x轴、y轴．若双曲线y=$\frac{x}{y}$与正方形ABCD有公共点，则k的取值范围为（　　）
    A．1＜k＜9B．2≤k≤34C．1≤k≤16D．4≤k＜16

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简，再求值：（a+1-$\frac{4a-5}{a-1}$）÷（$\frac{1}{a}$-$\frac{1}{{a}^{2}-a}$），其中a=2+$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，在菱形ABCD中，AD=2，点E在BC边上，将菱形ABCD沿直线AE折叠，点B恰巧落在AC上的点B′处，连接BE′，若BE′⊥BC，则AE=$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

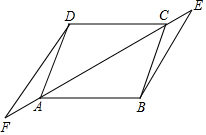    6．如图，?ABCD中，E，F是直线AC上两点，请在题目中添加合适的条件，就可以证明：BE=DF．
    （1）你添加的条件是AF=CE；
    （2）请你根据题目中的条件和你添加的条件证明BE=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知点A（m，m+1）和抛物线y=x2-2mx+m2+m-1上的动点P，其中m是常数，则线段AP的最小值是$\frac{\sqrt{7}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．在数学上，数370是一个水仙花数，水仙花数是自幂数的一种，自幂数是指一个n位数，它的每个位上的数字的n次幂之和等于它本身，例如三位数370=33+73+03，下列各数是自幂数的有①②⑤⑥（填写所有你认为正确的序号）．
    ①1；②9；③47；④361；⑤153；⑥371．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一元二次方程3x（x+1）=3x+3的两个实数根中较大的根为x=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若分式$\frac{x-1}{2x+5}$有意义，则x的取值范围是（　　）
    A．x≠1B．x$≠-\frac{5}{2}$C．x$＞-\frac{5}{2}$D．x$＜-\frac{5}{2}$

    查看答案和解析>>

    同步练习册答案