
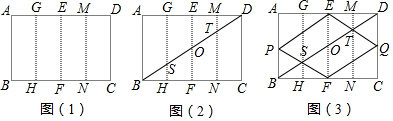
分析 (1)根据矩形性质得:AD=BC,AD∥BC,由对折性质可知:ED=BF,证明△EOD≌△FOB可得OE=OF;
(2)连接OA,由全等得:OB=OD,所以A、O、C共线,根据平行线分线段成比例定理得比例式得出DT=OT,根据一组对边平行且相等得四边形EPFQ为平行四边形,再利用△APE≌△DQE,得PE=EQ,由有一组邻边相等的平行四边形是菱形,得?EPFQ是菱形;
(3)添加AB=AD后,四边形EPFQ是正方形;证明△APE和△EQD是等腰直角三角形,得∠PEQ=90°,根据有一个角是直角的菱形是正方形得出结论.
解答 证明:(1)如图(2),∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
由折叠得:G、E、M将AD四等分,
∴ED=BF,
∵∠EOD=∠FOB,
∴△EOD≌△FOB,
∴OE=OF;
(2)由(1)得:△EOD≌△FOB,
∴OD=OB,
连接AC,
∴A、O、C共线,
∵GT∥EO,
∴$\frac{DG}{EG}=\frac{DT}{OT}$=1,
∴DT=OT,
∵AE=ED,OT=DT,
∴ET∥AC,ET=$\frac{1}{2}$AO,
即EQ∥AC,
同理得:TQ=$\frac{1}{2}$OC,
∴EQ=$\frac{1}{2}$AC,
同理得:PF=$\frac{1}{2}$AC,PF∥AC,
∴PF=EQ,PF=EQ,
∴四边形EPFQ是平行四边形,
∵PF∥AC,F是BC的中点,
∴P为AB的中点,
同理得:Q为DC的中点,
∴AP=QD=$\frac{1}{2}$AB,
∵AE=AD,∠BAD=∠ADC=90°,
∴△APE≌△DQE,
∴PE=EQ,
∴?EPFQ是菱形.
(3)当AB=AD时,四边形EPFQ是正方形,理由是:
∵E是AD的中点,P是AB的中点,
∴AE=$\frac{1}{2}$AD,AP=$\frac{1}{2}$AB,
∵AB=AD,
∴AP=AE,
∴△APE是等腰直角三角形,
∴∠AEP=45°,
同理∠QED=45°,
∴∠PEQ=90°,
由(2)得:四边形EPFQ是菱形,
∴四边形EPFQ是正方形;
故答案为:AB=AD.
点评 本题是四边形的综合题,考查了平行四边形、菱形、正方形的性质和判定、等腰直角三角形的性质和判定、三角形全等及平行线分线段成比例定理等知识,难度适中,熟练掌握特殊四边形的判定是关键.


科目:初中数学 来源: 题型:解答题
 2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!
2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,3cm,4cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 2cm,3cm,5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com