
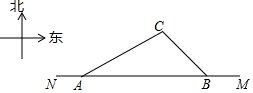
 2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!
2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!分析 (1)作CD⊥AB于点D,设CD=x,由∠CBA=45°知CD=BD=x,由AB=500知AD=500-x,根据tan∠CAD=$\frac{CD}{AD}$列方程求解可得;
(2)设2007和2008年两年绿化面积的年平均增长率为x,根据到2008年年底城区绿化面积达到72.6公顷,列出方程求解可得.
解答 解:(1)过点C作CD⊥AB于点D,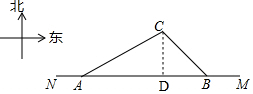
设CD=xm,
∵CD⊥AB,
∴∠CDB=90°,
∵∠CBA=45°,
∴∠DCB=∠CBA=45°,
∴CD=BD=x,
∵AB=500,
∴AD=500-x,
在Rt△ADC中,tan∠CAD=$\frac{CD}{AD}$,
即tan30°=$\frac{x}{500-x}$=$\frac{\sqrt{3}}{3}$,
解得x=$\frac{750(\sqrt{3}-1)}{3}$≈183>180,
∴不会穿过保护区;
(2)设2007和2008年两年绿化面积的年平均增长率为x,
根据题意得:60(1+x)2=72.6,
解得:x1=0.1 x2=-2.1(不符合题意,舍去),
答:2007年和2008年两年绿化面积的年平均增长率为10%.
点评 本题主要考查解直角三角形的应用及一元二次方程的应用,熟练掌握解关于仰角、俯角问题的直角三角形及一元二次方程中关于增长率问题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②③ | C. | ①②③⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
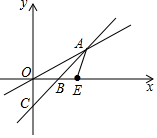 如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.
如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
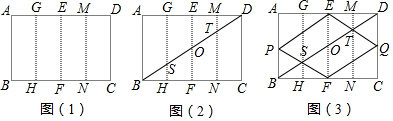
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com