
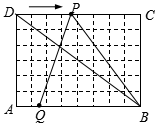
 如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?
如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形? 分析 根据△PQB成为以PQ为腰的等腰三角形分以下两种情况分别求解,①当PB=PQ时,由QP2=62+t2、PB2=62+(8-2t)2;②当QB=QP时,QP2=62+t2,QB=8-t;解出即可.
解答 解:作QS⊥FE于S,
根据题意知PD=2t,AQ=t,
则PS=2t-t=t,
在Rt△PSQ中,QP2=QS2+PS2,即QP2=62+t2,
①当PB=PQ时,QP2=62+t2,PB2=62+(8-2t)2;
解得,t=$\frac{8}{3}$或8(舍去);
②当QB=QP时,QP2=62+t2,QB=8-t;
解得,t=$\frac{7}{4}$;
故运动时间t为$\frac{8}{3}$或$\frac{7}{4}$秒时,△PQB成为以PQ为腰的等腰三角形.
点评 本题考查的是等腰三角形的判定,掌握等腰三角形的判定是解题的关键,注意分情况讨论思想的应用.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
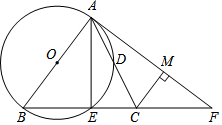 如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.
如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com