
 如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度.
如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度. 分析 先证E、B、C、A四点共圆,考虑到∠BAC=60°,于是以BC为边向上构造等边三角形,用同一法轻松得出结论,进而由∠DEC=∠DAC=30°得出E、D、C、A四点共圆,从而∠DCE=∠DAE=90°,再结合BC=4的已知条件即可算出答案.
解答 解:如图,以BC为边作等边三角形BCF,则F必在BC的中垂线上,
由∠BFC=∠BAC=60°可知F、B、C、A四点共圆,
连接FA,则∠FAB=∠FCB=60°=∠EAB,
∴点E、F重合,
∴E、A、C、B四点共圆,
∵∠CED=∠BAD=30°,
∴E、D、C、A四点共圆,
∴∠ECD=∠EAD=90°,
又∵BC=4,
∴ED=$\frac{8}{3}\sqrt{3}$.
点评 本题主要考查了三角形内外角平分线的性质、线段垂直平分线的性质、四点共圆的判断及性质、解直角三角形等重要知识点和方法,有一定难度.巧妙地证出E、B、C、A四点共圆是解决本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
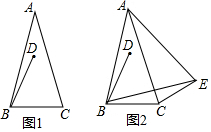 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
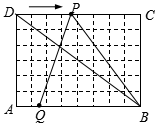 如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?
如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}{x^2}$-x=9 | B. | x3-x2+40=0 | C. | $\frac{4}{x-1}$=3 | D. | 3x3-2xy+y2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答:
将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com