
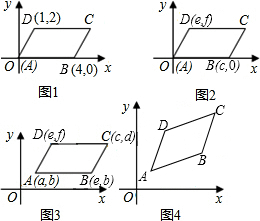
分析 (1)根据平行四边形的性质:对边平行且相等,得出图2,3中顶点C的坐标分别是(e+c,d),(c+e-a,d);
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,分别过A,B作AE⊥DD1于E,BF⊥CC1于点F.在平行四边形ABCD中,CD=BA,根据内角和定理,又因为BB1∥CC1,可推出∠EDA=∠FCB,△DEA≌△CFB.依题意得出AE=BF,DE=CF,设C(x,y).由x-1=2-1,得x=5.由y-2=3-1,得y=4,继而推出点C的坐标.
(3)在平行四边形ABCD中,CD=BA,同理证明△BEA≌△CFD(同(2)证明).然后推出AE=BF=a-c,DE=CF=d-b.又已知C点的坐标为(m,n),e-m=a-c,故m=e+c-a.由n-f=d-b,得出n=f+d-b.
解答 解:(1)利用平行四边形的性质:对边平行且相等,
得出图1、图2中顶点C的坐标分别是:(5,2)、(e+c,f),
故答案为:(5,2)、(e+c,f);
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,
分别过A,B作AE⊥DD1于E,BF⊥CC1于点F.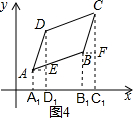
在平行四边形ABCD中,CD=BA,
又∵DD1∥CC1,
∴∠EDA+∠ADC+∠BCF=∠ABC+∠BCF+∠FCB=180度.
∴∠EDA=∠FCB.
又∵∠DEA=∠CFB=90°,
在△DEA与△CFB中,
$\left\{\begin{array}{l}{∠ADE=∠BF}\\{∠AED=∠BFC}\\{AD=BC}\end{array}\right.$,
∴△DEA≌△CFB,
∴AE=BF=2-1,DE=CF=3-1
设C(x,y).
由x-4=2-1,得x=5.
由y-2=3-1,得y=4,
∴C(5,4);
故答案为:(5,4)
(3)无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,
由(2)得:m=c+e-a,n=d+f-b或m+a=c+e,n+b=d+f.
故答案为:m=c+e-a,n=d+f-b.
点评 此题主要考查了平行四边形的性质,平面直角坐标系内的坐标,平行线的性质等知识.理解平行四边形的特点结合平面直角坐标系是解决本题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | m=8n | B. | m=8+6n | C. | m=4+4n | D. | m=2+6n |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2,则tan∠MCN=$\frac{3\sqrt{3}}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
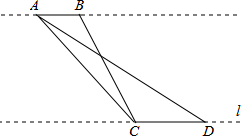 九(1)数学兴趣小组为了测量河对岸的古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,则古塔A、B的距离为$\frac{20\sqrt{3}}{3}$.
九(1)数学兴趣小组为了测量河对岸的古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,则古塔A、B的距离为$\frac{20\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com