
����Ŀ��Ϊ�ٿ������˶��ᣬѧУ��������һ�����������������3�������2��������420Ԫ������2�������4��������440Ԫ.
��1�������������ĵ��ۣ�
��2������ʵ����Ҫ��ѧУ�����������������100�������й����������������������������![]() ��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��3������������![]() ����ѧУ�������������������ܷ���Ϊ
����ѧУ�������������������ܷ���Ϊ![]() Ԫ���ڣ�2���������£������ַ�����ʹ
Ԫ���ڣ�2���������£������ַ�����ʹ![]() ��С�������
��С�������![]() ����Сֵ.
����Сֵ.
���𰸡���1������Ϊ100Ԫ������Ϊ60Ԫ����2����11�ֹ���.����3����������![]() ��СΪ7600Ԫ.
��СΪ7600Ԫ.
��������
��1����ÿ������xԪ��ÿ������yԪ�����������鼴�ɽ�����⣻
��2���蹺������m��������100-m��������������ʽ�飬�������⼴�ɣ�
��3������һ�κ���������һ�κ��������ʼ��ɽ������.
��1����ÿ������xԪ��ÿ������yԪ�������⣬�ã�
![]()
���![]()
������Ϊ100Ԫ������Ϊ60Ԫ.
��2���蹺������m��������100-m������������ɵã�
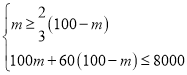
��ã�40��m��50��
��m��������
��m=40��41��42��43��44��45��46��47��48��49��50��
���11�ֹ�����
��3��������ɵ�y=100x+60��100-x��=40x+6000��40��x��50��
��k=40��0
��y��x�����������
�൱x=40ʱ��y����Сֵ��y��С=40��40+6000=7600��Ԫ��
���Ե�x=40ʱ��y����СֵΪ7600Ԫ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ľ�����̵ĺ�������գ�����������ע������
.��ͼ����֪��A=��F����C=��D����˵��BD��CE.

�⣺�ߡ�A=��F(��֪)
��AC��DF( )
���D=�� ( )
���ߡ�C=��D(��֪)
���1=��C(��������)
��BD��CE( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABC �У�ADƽ�֡�BAC��AE��BC����B��40�㣬��C��70�㣮
(1)���DAE�Ķ�����
(2)��ͼ�ڣ����ѡ�AE��BC����ɡ���F��DA���ӳ����ϣ�FE��BC���������������䣬���DFE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE��AC��CF��AB�ڵ�E��F��BE��CF���ڵ�D��DE=DF������AD��
��֤����1����FAD=��EAD��
��2��BD=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��P�ǡ�ABC�ı�BC�ϵ�һ���㣬��E���P����ֱ��AB����Գƣ�����EP��AB�ڵ�F������AP��EC�ཻ�ڵ�O������AE.

��1���ж�AE��AP��������ϵ����˵������.
��2���ڵ�P���˶������У���AE��BCʱ���ж�AP��BP��������ϵ����˵������.
��3������BAC=900����P���˶��������Ƿ�����߶�AP���߶�EC����ƽ�ֵ�����������ڣ��������P��λ�ã��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OΪԭ���ֱ������ϵ�У�����OABC������OC��OA�ֱ���x�ᡢy����������ϣ�����������![]() (x��0)��AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BD=3AD������ODE�������9,��k��ֵ��( )
(x��0)��AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BD=3AD������ODE�������9,��k��ֵ��( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������Ϸ��С��ӵ�A�������߶�AB�˶�����B��С���ӵ�C����������ͬ���ٶ��ء�O��ʱ���˶�һ�ܻص���C�����˵��˶�·����ͼ1��ʾ������AC![]() DB������ͬʱ��ʼ�˶���ֱ����ֹͣ�˶�ʱ��Ϸ����������������C�ľ���y��ʱ��x����λ���룩�Ķ�Ӧ��ϵ��ͼ2��ʾ��������˵����ȷ������������
DB������ͬʱ��ʼ�˶���ֱ����ֹͣ�˶�ʱ��Ϸ����������������C�ľ���y��ʱ��x����λ���룩�Ķ�Ӧ��ϵ��ͼ2��ʾ��������˵����ȷ������������


A. С����˶�·�̱�С���ij�
B. ���˷ֱ���1.09���7.49���ʱ������
C. ��С���˶�����D��ʱ��С���Ѿ������˵�D
D. ��4.84��ʱ�����˵ľ������õ��ڡ�O�İ뾶
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
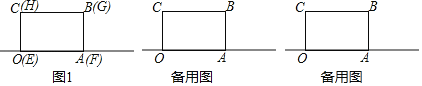
����Ŀ����������С��ȫһ���ij�����OABC��EFGH�غϷ���һ�𣬱�OA��EF�������ϣ�OΪ����ԭ�㣨��ͼ1����������OABC�ı߳�OA�ij�Ϊ6�����굥λ��
��1�������ϵ�A��ʾ����Ϊ�� ����
��2����������EFGH����������ֱ��ˮƽ�ƶ�
�����ƶ���ij�����EFGH�볤����OABC�ص����ֵ����ǡ�õ��ڳ�����OABC�����![]() �����ƶ����F�������ϱ�ʾ����Ϊ�� ����
�����ƶ����F�������ϱ�ʾ����Ϊ�� ����
��������EFGH����ˮƽ�ƶ���DΪ�߶�AF���е㣬������EFGH�ƶ�����xΪ��ֵʱ��D��E�����������ϱ�ʾ�����ǻ�Ϊ�෴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ���㣨0��2���ͣ�1����1������ͼ��Ķ�������ͶԳ��ᣮ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com