
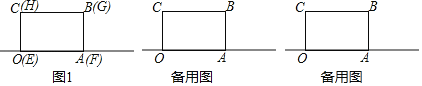
����Ŀ����������С��ȫһ���ij�����OABC��EFGH�غϷ���һ�𣬱�OA��EF�������ϣ�OΪ����ԭ�㣨��ͼ1����������OABC�ı߳�OA�ij�Ϊ6�����굥λ��
��1�������ϵ�A��ʾ����Ϊ�� ����
��2����������EFGH����������ֱ��ˮƽ�ƶ�
�����ƶ���ij�����EFGH�볤����OABC�ص����ֵ����ǡ�õ��ڳ�����OABC�����![]() �����ƶ����F�������ϱ�ʾ����Ϊ�� ����
�����ƶ����F�������ϱ�ʾ����Ϊ�� ����
��������EFGH����ˮƽ�ƶ���DΪ�߶�AF���е㣬������EFGH�ƶ�����xΪ��ֵʱ��D��E�����������ϱ�ʾ�����ǻ�Ϊ�෴����
���𰸡���1��6����2����2��10����x��4
��������
��1��OA��6�����������ϵ�A��ʾ������6��
��2�����ƶ���ij�����EFGH�볤����OABC�ص������dz����Σ��볤����OABC�ı�AB����һ�����ص����ֵ����ǡ�õ��ڳ�����OABC�����![]() �������ص�������һ����
�������ص�������һ����![]() OA��2��������������ۣ�����ƽ�ƺ�����ƽ�ƣ�
OA��2��������������ۣ�����ƽ�ƺ�����ƽ�ƣ�
��ƽ�ƺ�E��Ӧ�����ǩ�x����F��Ӧ������6��x�������е����깫ʽ��D��Ӧ������6��0.5x���ٸ��ݻ�Ϊ�෴������������Ϊ�㣬�з��̽�����⣮
�⣺��1����OA��6����A��ԭ����Ҳ�
�������ϵ�A��ʾ������6��
�ʴ�Ϊ��6��
��2�����ƶ���ij�����EFGH�볤����OABC�ص������dz����Σ��볤����OABC�ı�AB����һ�����ص����ֵ����ǡ�õ��ڳ�����OABC�����![]() ��
��
�����ص�������һ�߳�����![]() OA��2��������������ۣ�
OA��2��������������ۣ�
��������EFGH����ƽ��ʱ��OF��2����ԭ���Ҳ࣬
���Ե�F��ʾ������2��
��������EFGH����ƽ��ʱ��EA��2����AF��6��2��4��
����OF��OA+AF��6+4��10����F��ԭ���Ҳ࣬���Ե�F��ʾ������10.
�ʴ�Ϊ��2��10��
��������EFGH�����ƶ�����Ϊx����ƽ�ƺ�E��Ӧ�����ǩ�x����F��Ӧ������6��x��
��DΪ�߶�AF���е㣬
��D��Ӧ������![]() ��6��0.5x��
��6��0.5x��
ҪʹD��E�����������ϱ�ʾ�����ǻ�Ϊ�෴����
��x+6��0.5x��0��
��x��4.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ����������ʵʩ����������������ͥ�������ԵĹ滮.����������Ů�ĸ�����ͬ���ش�����������
��1������ͥ����һ���к���������һ�����ӣ����ڶ���������Ů���������� ��
��2���Ҽ�ͥû�к���������������������������һ��������Ů��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ٿ������˶��ᣬѧУ��������һ�����������������3�������2��������420Ԫ������2�������4��������440Ԫ.
��1�������������ĵ��ۣ�
��2������ʵ����Ҫ��ѧУ�����������������100�������й����������������������������![]() ��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��3������������![]() ����ѧУ�������������������ܷ���Ϊ
����ѧУ�������������������ܷ���Ϊ![]() Ԫ���ڣ�2���������£������ַ�����ʹ
Ԫ���ڣ�2���������£������ַ�����ʹ![]() ��С�������
��С�������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��x��0����y=ax+b��ͼ���ڵ�A����1��n���͵�B����2��1����
��x��0����y=ax+b��ͼ���ڵ�A����1��n���͵�B����2��1����
��1����k��a��b��ֵ��
��2��ֱ��x=m��![]() ��x��0����ͼ���ڵ�P����y=��x+1��ͼ���ڵ�Q������PAQ��90��ʱ��ֱ��д��m��ȡֵ��Χ��
��x��0����ͼ���ڵ�P����y=��x+1��ͼ���ڵ�Q������PAQ��90��ʱ��ֱ��д��m��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������C����C�ϵ�һ��A����ƽ���ڵĵ�P����������AP����C���ڵ�Q����Q�������P�غϣ�����![]() �����P��Ϊ��A������C�ġ������㡱��
�����P��Ϊ��A������C�ġ������㡱��
��֪��OΪ����ԭ������O�İ뾶Ϊ1����A��-1��0����
��1������P�ǵ�A���ڡ�O�ġ������㡱���ҵ�P��x��������д��һ�����������ĵ�P������________��
��2������B�ǵ�A���ڡ�O�ġ������㡱��������![]() �����B��������t��ȡֵ��Χ��
�����B��������t��ȡֵ��Χ��
��3��ֱ��![]() ��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
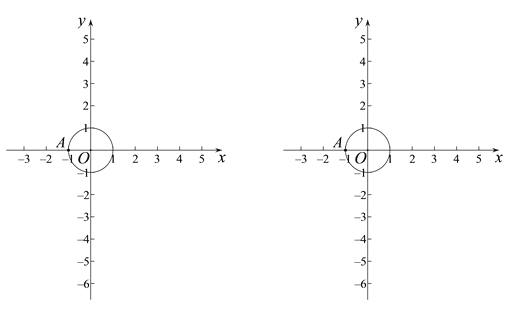
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף�����ͬѧ�����г���A����ͬһ��·��B������֪�ұȼ��ȳ���������������صľ���S��km��������ʱ��t��h��֮��ĺ�����ϵ��ͼ1��ʾ����������˵���������Ƕ�������20km��������;��ͣ����0.5h�����ף�������ͬʱ����Ŀ�ĵ����������������ٶ�С���ҵ��ٶ���
����ͼ����Ϣ������˵����ȷ������������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����������赸����ֽ�����γ̣�Ϊ���˽�ѧ�����������γ̵���Ȥ����������ȡ�˲���ѧ�����е��飨ÿ�˴���ֻ��ѡһ�������������������Ƴ���������ͳ��ͼ��������ͼ����Ϣ������⣮

��1��������ͳ��ͼ����������
��2������������������������ ����
��3��������ͳ��ͼ�У���Ů��ϲ����ֽ��γ�������Ӧ��Բ�ĽǶ�����
��4����֪��У��1200��ѧ������ȫУѧ����ϲ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����X��һԪ���η���Ϊ�� ![]() ��
��
��1������������ʵ����ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ȡһ��![]() ֵ��������̵����������ʵ������
ֵ��������̵����������ʵ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com