
【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(1)求k,a,b的值;
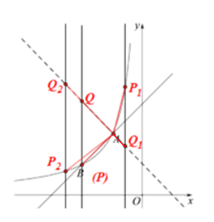
(2)直线x=m与![]() (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.

【答案】(1)k=﹣2,a=1,b=3;(2)当m<﹣2或﹣1<m<0时,∠PAQ>90°.
【解析】试题分析:
(1)把点B的坐标代入![]() 即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数
即可求得k的值;再把点A的坐标代入所得反比例函数的解析式即可求得n的值;把A、B的坐标代入一次函数![]() 列出方程组,解方程组即可求得a、b的值;
列出方程组,解方程组即可求得a、b的值;
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),由此可得:直线
,点A的坐标为(-1,2),由此可得:直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,即∠QAB=90°,由下图可知,①当直线
,垂足为点A,即∠QAB=90°,由下图可知,①当直线![]() 在点B的左侧时,∠PAQ<90°;②当直线
在点B的左侧时,∠PAQ<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当
在点A右侧,原点左侧时,∠P1AQ1>90°.综合可得当![]() ,且
,且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.
试题解析:
(1)∵ 函数![]() (
(![]() )的图象经过点B(-2, 1),
)的图象经过点B(-2, 1),
∴![]() ,得
,得![]() .
.
∵ 函数![]() (
(![]() )的图象还经过点A(-1,n),
)的图象还经过点A(-1,n),
∴![]() ,点A的坐标为(-1,2).
,点A的坐标为(-1,2).
∵ 函数![]() 的图象经过点A和点B,
的图象经过点A和点B,
∴![]() 解得
解得![]()
(2)如下图,由(1)可知一次函数![]() 的解析式为:
的解析式为: ![]() ,点A的坐标为(-1,2),
,点A的坐标为(-1,2),
∴直线![]() 过点A,且直线
过点A,且直线![]() 垂直于直线
垂直于直线![]() ,垂足为点A,
,垂足为点A,
∴∠QAB=90°,
结合图形和已知条件分析可知,∠QAB的大小存在以下情形:①当直线![]() 在点B的左侧时,∠P2AQ2<90°;②当直线
在点B的左侧时,∠P2AQ2<90°;②当直线![]() 过点B时,∠PAQ=90°;③当直线
过点B时,∠PAQ=90°;③当直线![]() 在点B的右侧,点A左侧时,∠PAQ>90°;④当直线
在点B的右侧,点A左侧时,∠PAQ>90°;④当直线![]() 过点A时,P、A、Q三点重合;⑤当直线
过点A时,P、A、Q三点重合;⑤当直线![]() 在点A右侧,原点左侧时,∠P1AQ1>90°;
在点A右侧,原点左侧时,∠P1AQ1>90°;
综上所述,当![]() 且
且![]() 时,∠PAQ>90°.
时,∠PAQ>90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某广场上一个形状是平行四边形的花坛,分别种有红、黄、蓝、白、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )
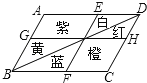
A.红花,白花种植面积一定相等
B.红花,蓝花种植面积一定相等
C.蓝花,黄花种植面积一定相等
D.紫花,橙花种植面积一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
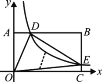
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC![]() DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )


A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
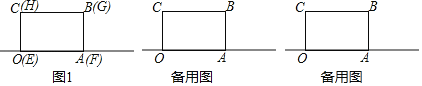
【题目】有两个大小完全一样的长方形OABC和EFGH重合放在一起,边OA、EF在数轴上,O为数轴原点(如图1),长方形OABC的边长OA的长为6个坐标单位.
(1)数轴上点A表示的数为 .
(2)将长方形EFGH沿数轴所在直线水平移动
①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的![]() ,则移动后点F在数轴上表示的数为 .
,则移动后点F在数轴上表示的数为 .
②若出行EFGH向左水平移动后,D为线段AF的中点,求当长方形EFGH移动距离x为何值时,D、E两点在数轴上表示的数是互为相反数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前2个小时为生产磨合期,2个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式,他们每人生产的零件总数![]() (个)与生产时间
(个)与生产时间![]() (小时)的关系如图所示,根据图象回答:
(小时)的关系如图所示,根据图象回答:
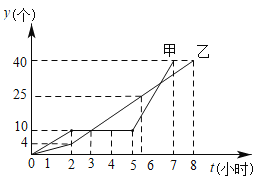
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时?
(2)当![]() 为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
(3)设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团上午6时从旅馆出发,乘汽车到距离210km的著名旅游景点游玩,已知该汽车离旅馆的距离S(km)与时间t(h)的关系如图所示,根据图像提供的信息,解答以下问题:

(1)求该旅行团在景点游玩了多少小时?
(2)求该旅行团去景点的平均速度?
(3)求返回宾馆时该汽车离旅馆的距离S(km)与时间t(h)的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com